Пусть количество белых шариков равно Б, черных - Ч. Ясно, что хотя бы одно из этих чисел больше или равно 2, поскольку речь идет о двух одноцветных шариках. При этом минимальное количество шариков, которые нужно вынуть, чтобы получить 2 одноцветных, равно 3 (первые 2 могут быть разноцветными, третий совпадет с одним из первых двух). С другой стороны, чтобы гарантировано получить 2 разноцветных шарика, нужно взять max(Б,Ч) +1 шарик. Значит,
max(Б,Ч)+1=3, max(Б,Ч)=2.
Итак, возможны ситуации: Б=2, Ч=1 (симметричная ситуация Ч=2, Б=1), а также Б=Ч=2.
Пусть количество белых шариков равно Б, черных - Ч. Ясно, что хотя бы одно из этих чисел больше или равно 2, поскольку речь идет о двух одноцветных шариках. При этом минимальное количество шариков, которые нужно вынуть, чтобы получить 2 одноцветных, равно 3 (первые 2 могут быть разноцветными, третий совпадет с одним из первых двух). С другой стороны, чтобы гарантировано получить 2 разноцветных шарика, нужно взять max(Б,Ч) +1 шарик. Значит,
max(Б,Ч)+1=3, max(Б,Ч)=2.
Итак, возможны ситуации: Б=2, Ч=1 (симметричная ситуация Ч=2, Б=1), а также Б=Ч=2.
a) cos(a-b) - cos(a+b) = cos(a)*cos(b) + sin(a)*sin(b) - (cos(a)*cos(b) - sin(a)*sin(b)) = cos(a)*cos(b) + sin(a)*sin(b) - cos(a)*cos(b) + sin(a)*sin(b) = 2sin(a)*sin(b)
b) sin(2a) + cos(2a) + 1 = 2*sin(a)*cos(a) + cos²(a) - sin²(a) + cos²(a) + sin²(a) = 2*sin(a)*cos(a) + 2*cos²(a) = 2*cos(a)*(sin(a) + cos(a))
sin(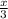 ) = -
) = -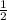
или
x₁ = -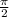 + 6πκ, κ∈Ζ
+ 6πκ, κ∈Ζ
x₂ =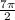 + 6πn, n∈Ζ
+ 6πn, n∈Ζ
Отбор корней произведем с неравенств.
x₁: 0 ≤ -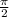 + 6πκ ≤ 3π
+ 6πκ ≤ 3π
Так как κ∈Ζ, то κ∈∅
x₂: 0 ≤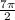 + 6πn ≤ 3π
+ 6πn ≤ 3π
-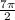 ≤ 6πn ≤ 3π -
≤ 6πn ≤ 3π - 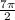
-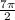 ≤ 6πn ≤ -
≤ 6πn ≤ - 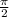
-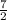 ≤ 6n ≤ -
≤ 6n ≤ - 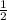
-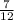 ≤ n ≤ -
≤ n ≤ - 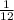
Так как n∈Ζ, то n∈∅ ⇒ нет корней на данном промежутке