а) 8170
б) ≈ 0,71
Объяснение:
а)
Количество выбора m элементов из n - это число сочетаний из n по m:
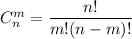
Девочек должно быть не меньше трех. Значит возможны варианты выбора семи школьников в комитет:
3 девочки из семи и 4 мальчика из девяти (применяем правило произведения):
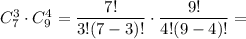
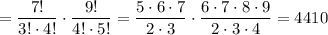
4 девочки и 3 мальчика:
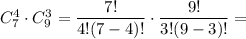
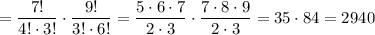
5 девочек и 2 мальчика:
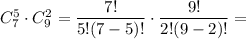
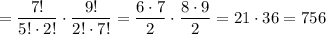
6 девочек и 1 мальчик:
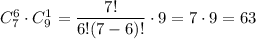
и, наконец, все 7 человек - девочки .
По правилу суммы:
4410 + 2940 + 756 + 63 + 1 = 8170 - количество выбрать 7 человек в комитет так, чтобы в нем было не менее трех девочек.
б)
Всего школьников: 9 + 7 = 16 человек.
Количество выбрать 7 человек из шестнадцати:
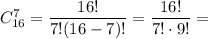
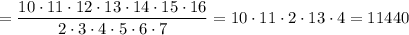
Вероятность того, что в комитете будет не менее трех девочек:
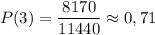
Даны координаты вершин пирамиды:
А1 (-10; 6; 6), А2 (-2; 8; 2), А3 (5; -7; 4), А4 (-4; 10; 9).
Найти:
1) угол между ребрами А1А2 и А1А4.
Находим векторы А1А2 и А1А4.
А1А2 = (-2-(-10); 8-6; 2-6) = (8; 2; -4), модуль равен √(64+4+16) = √84 = 2√21.
А1А4 = (-4-(-10); 10-6; 9-6) = (6; 4; 3), модуль равен √(36+16+9) = √61.
Находим косинус угла (А1А2_А1А4):
cos (А1А2_А1А4) = (8*6+2*4+(-4)*3)/( 2√21*√61) = 44/(2√1281) = 22√1281/1281.
Угол (А1А2_А1А4) = arccos(22√1281/1281) = arccos 0,614679 = 0,90882 радиан или 52,0714 градуса.
2) уравнение прямой А1А2.
По точке А1 (-10; 6; 6) и вектору А1А2(8; 2; -4) составляем уравнение:
(x + 10)/8 = (y – 6)/2 = (z – 6)/(-4).