8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то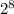 
сравнимо с 1 по модулю 15.
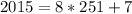
Тогда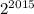 
можно записать в виде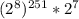 
Поскольку мы выяснили, что 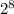сравнимо с 1 по модулю 15, то 
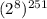также сравнимо с 1 по модулю 15.
Остаётся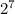 
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: 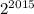≡ ≡ 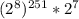≡ 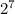8 mod 15
Это значит, что остаток равен 8.
Пусть с помидорами было х банок, тогда с огурцами - 2х банок
(2х-4):(х-6)=3:1
Применяем основное свойство пропорции: произведение крайних членов равно произведению средних.
2х-4=3(х-6)
2х-4=3х-18
2х-3х=4-18
-х=-14
х=14
ответ. 14 банок с помидорами и 28 банок с огурцами было.
2.Пусть х людей было на регистрации и у машин
Предложение "если в каждую машину сядет по три гостя, то двоим не хватит места" дает возможность составить первое уравнение:
3у+2=х
Предложение "если по четыре, то три места останутся свободными" дает возможность составить второе уравнение:
4у-3=х
получаем систему
ответ. 5 машин и 17 приглашенных