30 кг
Объяснение:
Пусть «
» кг раствора было изначально ⇒ 
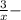доля соли в этом растворе ⇒ 
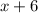кг раствора стало после добавления соли ⇒ 
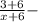доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (
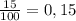), получим:
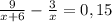
Домножим обе части уравнения на и 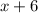, получим:
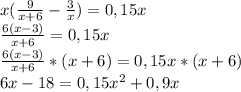
Перенесём правую часть уравнения в левую, получим:
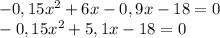
Квадратное уравнение вида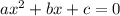 
можно решить с дискриминанта 
.
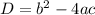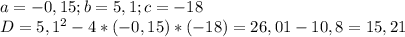
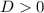⇒ корней будет два.
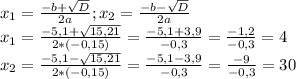
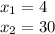
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒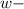 
(массовая доля соли в первоначальном растворе) должна быть 
.
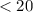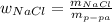* 100%
⇒ 
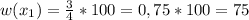
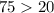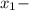не является решением.
⇒ 
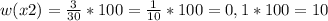
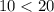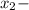является решением.
Значит, первоначальная масса раствора была 30 кг.
Имеются три графика: парабола, гипербола и прямая.
График под буквой А - парабола.
Среди данных функций параболу задаёт лишь одна функция - это
функция y=x² под номером 3. Значит, первое соответствие: А-3
График под буквой Б - гипербола.
Среди данных функций гиперболу задаёт лишь одна - это
функция y=2/x под номером 2. Значит, второе соответствие: Б-2
График под буквой В - прямая
Среди данных функций прямую задаёт лишь одна - это
функция y=х/2 под номером 1. Значит, третье соответствие: В-1
Внесём эти данные в таблицу:
А Б В
3 2 1
1) Нет корней
2) -√2, √2