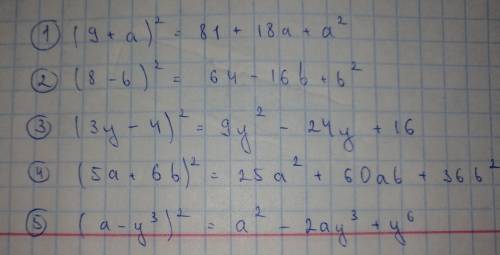
ответ: h(t) = 9t - 2t², h - высота в м, t - время в секундах.
а) На какой высоте будет мяч через 2 секунды
t=2
h(2)=9*2-2*2²=10 метров
б) Через сколько секунд мяч будет находиться на высоте 10 м?
h=10
9t--2t²=10
2t²-9t+10=0
D=9²-4*2*10=1
t₁=(9-1)/4=2 с
t₂=(9+1)/4=2.5 с
Значит на высоте 10 м мяч буде находится через 2 с и через 2,5 с
в) Какой наибольшей высоты достиг мяч?
h(t) = 9t - 2t² парабола, ветви направлены вниз, значит точка максимума в вершине параболы:
t₀=-9/(-2*2)=2.25 c
h(2.25)=9*2.25-2*2.25²=20.25-10.125=10.125 м максимальная высота
Объяснение:надеюсь поймёшь
7/Задание № 1:
Сколько чётных двузначных чисел, которые при делении на сумму цифр числа дают неполное частное 7 и остаток 3?
РЕШЕНИЕ: Пусть это число АВ=10a+b. Тогда, 10a+b=7(a+b)+3.
10a+b=7a+7b+3
3a=6b+3
a=2b+1
2b=a-1
Учитывая, что:
- а и b цифры, то есть целые числа от 0 до 9, но а не ноль, поскольку AB двузначное число
- число AB должно быть четным, то проверять нечетные b нет смысла
- остаток должен быть меньше делителя, значит минимально возможная сумма (a+b) равна 4
b=0: a=2*0+1=1 - не может быть a+b=1<4
b=2: a=2*2+1=5, число 52
b=4: a=2*4+1=9, число 94
При b=6 и более а=2*6+1=13 и более - не соответствует цифре.
ОТВЕТ: 2 числа
7/Задание № 3:
Сколько корней имеет уравнение: |x+2+|−x−4||−8=x?
|x+2+|−x−4||−8=x
|x+2+|x+4||−8=x
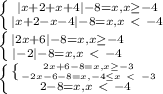
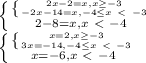
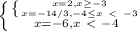
Условию раскрытия моделей соответствуют только первый и третий корни 2 и -6.
ОТВЕТ: 2 корня