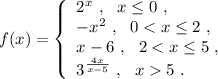
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
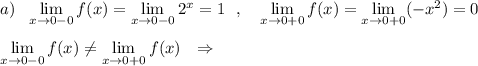
При х=0 функция имеет разрыв 1 рода .
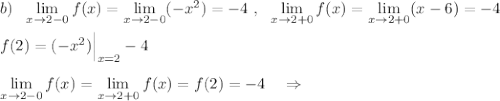
При х=2 функция непрерывна.
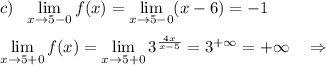
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
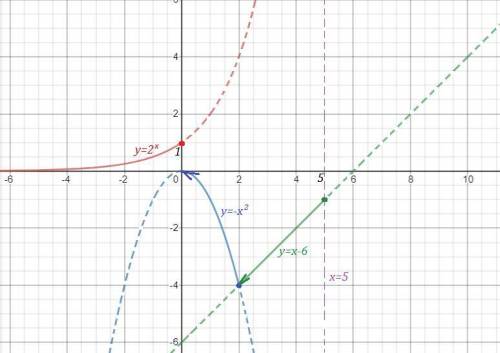
На 1 рисунке нет чертежа функции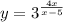 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
Функция задана уравнением y = x² – 4x - 5
Это парабола ,ветви вверх. Область определения :х-любое, множество значений функции [ -9; +∞) ;
а) Найдите вершину параболы
х₀=-в/2а, х₀=-(-4)/2= 2 , у₀=2²-4*2 -5= -9 , ( 2; -9).
Тогда наименьшее значение функции у=-9 ( при х=2)
Наибольшего значения нет ;
b) В какой точке график данной функции пересекает ось ОY.
Точки пересечения с оу ( х=0)
у= 0²- 4*0-5=-5, Точка (0; -5).
c) Найдите точки пересечения графика функции с осью ОХ.
Точки пересечения с осью ох( у=0)
x²- 4x-5=0 , Д=36 , х₁=(4+6)/2=5, х₂=(4-6)/2=-1. Точки (5;0) , ( -1;0).
d) Запишите уравнение оси симметрии графика данной функции :
х=2.
e) Постройте график функции.Смотри ниже
f) Найдите промежутки возрастания убывания функции
Функция убывает при х≤ 2 ,
функция возрастает при x≥2;
Промежутки знакопостоянства функции :
+ . - .+
______(-1)_______(5)_______
у>0 при х <-1 и x>5
у<0 при -1 <х< 5 ;
Доп. точки у= x²- 4x-5:
х: -2 1 6
у: 7 -8 7