Приравняем многочлены (x + 1)^2 и 7x - 3x^2, и решим получившееся уравнение.
(x + 1)^2 = 7x - 3x^2 - раскроем скобку, применив формулу квадрата двучлена (a + b)^2 - a^2 + 2ab + b^2, где a = x, b = 1;
x^2 + 2x + 1 = 7x - 3x^2 - перенесем слагаемые из правой части уравнения в левую; при переносе слагаемых из одной части уравнения в другую, знаки переносимых слагаемых меняются на противоположные;
x^2 + 2x + 1 - 7x + 3x^2 = 0;
(x^2 + 3x^2) + (2x - 7x) + 1 = 0;
4x^2 - 5x + 1 = 0;
D = b^2 - 4ac;
D = (-5)^2 - 4 * 4 * 1 = 25 - 16 = 9; √D = 3;
x = (-b ± √D)/(2a);
x1 = (5 + 3)/(2 * 4) = 8/8 = 1;
x2 = (5 - 3)/8 = 2/8 = 1/4.
ответ. 1; 1/4.
Объяснение:
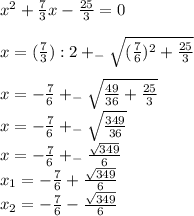
сверху первый. В примере а) 2 корня. (я расписала подробно, но ты можешь решить так как я решила пример в б)
Б) D= 1^2-4*2*5
D=-39
корней нет.
2. а) D=(-11)^2-4*1*(-42) = 289 = 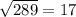
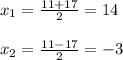
б) решу методом замены переменной:
y^2-13y+36=0
D=(-13)^2-4*36=25= 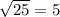
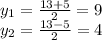
x^2=9 x^2=4
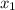 =-3;
=-3; 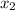 =-2;
=-2; 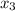 =2;
=2; 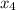 =3.
=3.
в) D=5^2-4*2*2 = 25-16 = 9 = 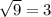
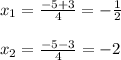
3. Длина первого катета - х см, тогда длина второго катета
будет (х + 5) см.
Площадь прямоугольного треугольника вычисляется по формуле:
S = 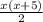
x*(x + 5) = 42*2
x² + 5x - 84 = 0
D = 25 + 4*1*84 = 361 = 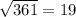
x₁ = (- 5 - 19)/2
x₁ = - 24/2 = - 12 посторонний корень
x₂ = (- 5 + 19)/2
x₂ = 7
7 см - длина первого катета
1) 7 + 5 = 12 (см) - длина второго катета
ответ: 7 см, 12 см
log3/5((2x+3)/(x-2)=1
log3/5((2x+3)/(x-2)=log3/5(3/5)
(2x+3)/(x-2)=3/5
3(x-2)=5(2x+3)
3x-6=10x+15
7x=-21
x=-3
Проверка: (2*(-3)+3)/(-3-5)=-3/(-8)=3/8>0 значит -3 входит в ОДЗ
ответ: x=-3