а) x€ (-∞;-4)U(2;+∞)
б) x€∅
Объяснение:
N°1:
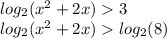
Т. к. основание логарифма 2 > основание 1 => знак неравенства не меняется
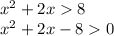
D = b²-4ac = 4+32 = 36 = 6²
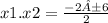
х1= 2; х2 = -4
(х-2)(х+4) > 0
х€ (-∞; -4)U(2;+∞)
ОДЗ: х²+2х > 0
х(х+2) > 0
Значит:
х€ (-∞; -2)U(0;+∞)
Получаем систему:
{x€ (-∞;-4)U(2;+∞)
{x € (-∞;-2)U(0;+∞)
Отсюда:
x€ (-∞;-4)U(2;+∞)
ответ: x€ (-∞;-4)U(2;+∞)
N°2:
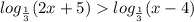
Т. к основание логарифма 1/3 < основания 1 => знак неравенства меняется
2х+5 < х-4
х <-9
Значит:
х€ (-∞; -9)
ОДЗ:
{2х+5 > 0
{х-4 > 0
Получаем:
{х> -2,5
{х>4
Значит:
х€ (4;+∞)
Получаем систему:
{х€ (-∞;-9)
{х€ (4;+∞)
Отсюда: х€∅
ответ: х€∅
у²-3у - 1 = у² - 2 *1,5 у + (1,5)² - 3,25= (у-1,5)²- 3,25
если у² -3у -1 = 11 , следовательно :
(у-1,5)² - 3,25=11
(у-1,5)²= 11+3,25
(у-1,5)²=14,25
Теперь выделим неполный квадрат из второго выражения:
8у²- 24у - 9 = 8 (у²- 3у - 9/8 ) = 8(у²-3у -1,125) =
= 8 ( у² -3у + 2,25 - 3,375) = 8 (( у-1,5)² - 3,375 ) =
= 8(у-1,5)² - 8 * 3,375 = 8(у-1,5)² - 27
если (у-1,5)²=14,25 , то из второго выражения получается:
8*14,25 -27 = 114-27 = 87
ответ: если у²-3у-1=11 , то 8у²-24у -9 = 87.