Алгебра: 6/х в квадрате-9 + 1/3-х) * х в квадрате+6х+9/5

- это правая полуокружность от окружности с центром в точке (0,0) и R=2 , выразим , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) . - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её. Найдём точки пересечения окружности и параболы....

6/х в квадрате-9 + 1/3-х) * х в квадрате+6х+9/5

👇

Увидеть ответ

Ответ:

Егор4002

07.07.2021

$(\frac{6}{ x^{2} -9} + \frac{1}{3-x})* \frac{ x^{2} +6x+9}{5}=(\frac{6}{(x-3)(x+3)}- \frac{1}{x-3})* \frac{(x+3)(x+3) }{5}= \\ \\ \frac{6-x-3}{(x-3)(x+3)}* \frac{(x+3)(x+3)}{5}= \frac{-(x-3)(x+3)}{5(x-3)}=- \frac{x+3}{5}$

4,6(30 оценок)

Открыть все ответы

Ответ:

Tolapula

07.07.2021

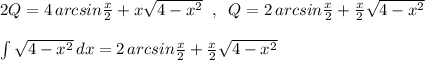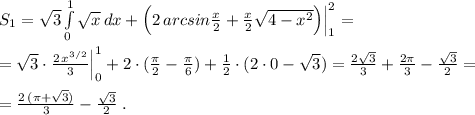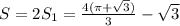
В Китае, как ты знаешь, и сам император и все его подданные — китайцы. Дело было давно, но потому-то и стоит о нём послушать, пока оно не забудется совсем! В целом мире не нашлось бы дворца лучше императорского; он весь был из драгоценного фарфора, зато такой хрупкий, что страшно было до него дотронуться. В саду росли чудеснейшие цветы; к самым лучшим из них были привязаны серебряные колокольчики; звон их должен был обращать на цветы внимание каждого прохожего. Вот как тонко было придумано! Сад тянулся далеко-далеко, так далеко, что и сам садовник не знал, где он кончается. Из сада можно было попасть прямо в густой лес; в чаще его таились глубокие озёра, и доходил он до самого синего моря. Корабли проплывали под нависшими над водой вершинами деревьев, и в ветвях их жил соловей, который пел так чудесно, что его заслушивался, забывая о своём неводе, даже бедный, удручённый заботами рыбак. «Господи, как хорошо!» — вырывалось наконец у рыбака, но потом бедняк опять принимался за своё дело и забывал о соловье, на следующую ночь снова заслушивался его и снова повторял то же самое: «Господи, как хорошо!»не

4,5(49 оценок)

Ответ:

mrtwesor

07.07.2021

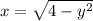$x=\sqrt{4-y^2}$ - это правая полуокружность от окружности 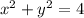x^2+y^2=4 с центром в точке (0,0) и R=2 , выразим 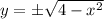$y=\pm \sqrt{4-x^2}$ , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .

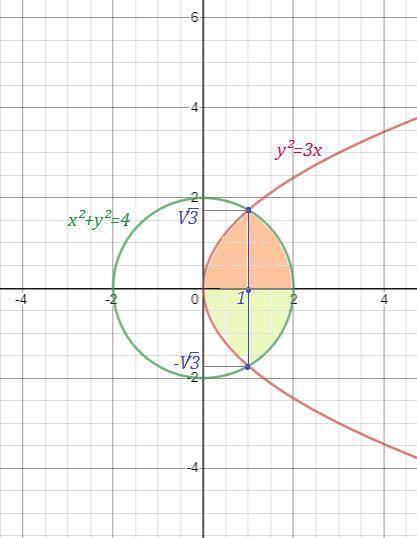
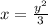$x=\frac{y^2}{3}$ - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: 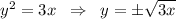$y^2=3x\; \; \Rightarrow \; \; y=\pm \sqrt{3x}$ , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.

Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её.

Найдём точки пересечения окружности и параболы.

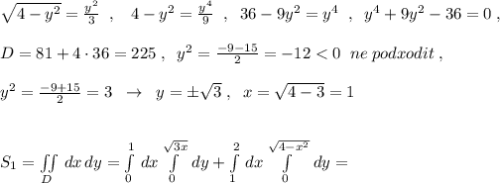
$\sqrt{4-y^2}=\frac{y^2}{3}\; \; ,\; \; \; 4-y^2=\frac{y^4}{9}\; \; ,\; \; 36-9y^2=y^4\; \; ,\; \; y^4+9y^2-36=0\; ,\\\\D=81+4\cdot 36=225\; ,\; \; y^2=\frac{-9-15}{2}=-12$

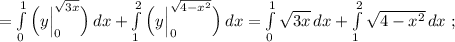
$=\int\limits^1_0\Big (y\Big |_0^{\sqrt{3x}}\Big)\, dx+\int \limits _1^2\Big (y\Big |_0^{\sqrt{4-x^2}}\Big)\, dx=\int\limits^1_0\sqrt{3x}\, dx+\int\limits^2_1\sqrt{4-x^2}\, dx\; ;$

$Q=\int \sqrt{4-x^2}\, dx\\\\Q=\int \frac{4-x^2}{\sqrt{4-x^2}}\, dx=4\int \frac{dx}{\sqrt{4-x^2}}-\int \frac{x\, \cdot \, x\, dx}{\sqrt{4-x^2}}=\Big[\; u=x\; ,\; du=dx\; ,\\\\dv=\frac{x\, dx}{\sqrt{4-x^2}}\; ,\; v=-\frac{1}{2}\cdot 2\sqrt{4-x^2}=-\sqrt{4-x^2}\; ,\; \int u\, dv=uv-\int v\, du\; \Big]=\\\\=4\cdot arcsin\frac{x}{2}-\Big(-x\sqrt{4-x^2}+\int \sqrt{4-x^2}\, dx\Big)=\\\\=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; \Rightarrow \; \; Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; ,$

$2Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}\; \; ,\; \; Q=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\\\\\int \sqrt{4-x^2}\, dx=2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}$

$S_1=\sqrt3\int \limits _0^1\sqrt{x}\, dx+\Big(2\, arcsin\frac{x}{2}+\frac{x}{2}\sqrt{4-x^2}\Big)\Big|_1^2=\\\\=\sqrt3\cdot \frac{2\, x^{3/2}}{3}\Big|_0^1+2\cdot (\frac{\pi}{2}-\frac{\pi}{6})+\frac{1}{2}\cdot (2\cdot 0-\sqrt3)=\frac{2\sqrt3}{3}+\frac{2\pi }{3}-\frac{\sqrt3}{2}=\\\\=\frac{2\, (\pi +\sqrt3)}{3}-\frac{\sqrt3}{2}\; .$