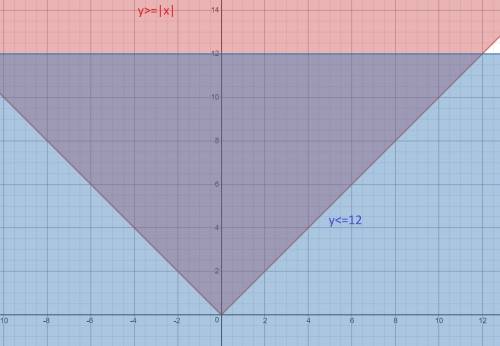
Х равен от минус бесконечности до плюс бесконечности (-∞;+∞) (у Х такое значение, ведь нам не дали никаких условий для его определения)
У равен от 0 до 12 включительно, ведь из-за модуля У не будет больше 0, но и из-за другого условия (у≤12) поэтому [0;12] но, наверное, тебе нужен лишь У
Объяснение:
1.Функция -отношение между элементами, при котором изменение в одном элементе влечёт изменение в другом.Область определения функции-множество, на котором задаётся функция.
2. Начальная функция это y0. Неопределенный интеграл-это совокупность всех первообразных данной функции.
Свойства неопределенного интеграла
1)Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3)Постоянный множитель можно вынести из-под знака интеграла, т.е. если то
4)Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.
Интегрирование- название, данное ряду приемов, используемых для вычисления различных ИНТЕГРАЛОВ.
3.

|x|≥0 по определению.
|x|≤y; y не может быть меньше нуля т.к. модуль не может быть меньше нуля, минимальное значение х это 0. Значит y≥0. Безусловно можно рассматривать и при других значениях X, но все последующие значения Y будут объединены вместе как одно, и при этом Y всегда будет больше какого-то числа, которое ≥ 0. А потом всё это просто пересекается со вторым утверждение y≤0. Выглядит это так:
В итоге получается 0≤y≤12
ответ: y∈[0;12]
Так же смотри наглядный график.