На вопрос о количестве участников командного соревнования по ма-тематике председатель оргкомитета ответил, что приняло участие 55 человек, из которых 13 девушек, а председатель жюри сказал, что участников всего 31 и среди них 24 юноши. как это может быть и сколько всего участников?
ответы даны в различных системах счисления.
1) Числа 55 и 13 даны в -ичной системе счисления:
-ичной системе счисления:
Максимальная цифра данных чисел - 5, значит, система счисления может содержать не менее 6 цифр (от 1 до 5 и 0), это означает, что оно может быть записано в шестиричной и выше системах счисления.
Получаем ОДЗ для х. => x≥6
2) Аналогично для чисел 31 и 24, которые даны в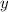 -ичной системе счисления:
-ичной системе счисления:
Максимальная цифра данных чисел - 4, значит, система счисления может содержать не менее 4 цифр (от 1 до 4 и 0), это означает, что оно может быть записано в пятиричной и выше системах счисления.
Получаем ОДЗ для у. => у≥5
3) Берем числа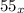 и
и 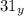 , обозначающие одну и ту же величину.
, обозначающие одну и ту же величину.
Получаем уравнение:
А далее методом подбора, учитывая ОДЗ x≥6 и у≥5; x;y-целые числа.
..............................................................................
Получаем
4)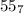 =5*7+5=40
=5*7+5=40
Всего 40 участников.