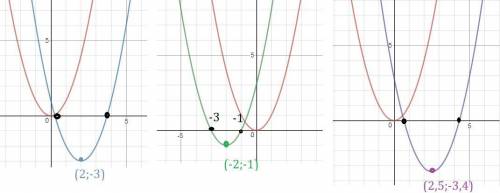
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
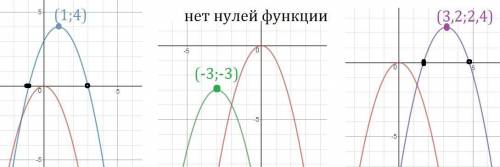
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
См. Объяснение
Объяснение:
Это связано с тем, какой общий знаменатель у этих трёх дробей.
Чтобы найти общий знаменатель, необходимо:
1) знаменатель каждой дроби разложить на множители:
а) знаменатель первой дроби уже представлен в виде произведения;
b) знаменатель второй дроби: (1+z)² = (1+z)·(1+z)
с) знаменатель третьей дроби: (1-z)² = (1-z)·(1-z)
2) находим общий знаменатель - такое наименьшее выражение, которое делится на знаменатель каждой из 3-х дробей:
Общий знаменатель = (1-z)·(1+z)·(1+z)·(1-z) = (1+z)²·(1-z)²
Здесь (1-z)·(1+z) - от первой дроби; (1+z) добавили от 2-й дроби, чтобы общий знаменатель делился на (1+z)²; (1-z) добавили от 3-й дроби, чтобы общий знаменатель делился на (1-z)².
3) находим дополнительные множители:
а) к первой дроби:
(1-z)·(1+z)·(1+z)·(1-z) : (1-z)·(1+z) = (1+z)·(1-z)
b) ко второй дроби:
(1-z)·(1+z)·(1+z)·(1-z) : (1+z)·(1+z) = (1-z)·(1-z) = (1-z)²
с) к третьей дроби:
(1-z)·(1+z)·(1+z)·(1-z) : (1-z)·(1-z) = (1+z)·(1+z) = (1+z)²
4) после перемножения получаем в числителе:
3 · (1+z)·(1-z) - 2 · (1-z)² + 5 · (1+z)²
во вложении ответ_________