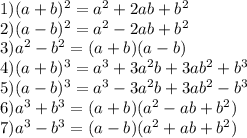
к 1 формулe:
(x+y)^2
(2a+3)^2
(5+2c)^2
(a+2)^2
(1+5a)^2
(3+2a)^2
(4+2z)^2
(2x+3y)^2
(x+3)^2
(p+q)^2
ко 2 формуле:
(x-y)^2
(2a-3)^2
(5-2c)^2
(a-2)^2
(1-5a)^2
(3-2a)^2
(4-2z)^2
(2x-3y)^2
(x-3)^2
(p-q)^2
к 3 формуле:
25a^2-9b^2
16-a^2
36x^2-25y^2
x^2-1
81-9a^2
16x^2-100y^2
y^2-49
x^2-y^2
a^2-4b^2
a^2-16b^4
к 4 формуле:
(n+q)^3
(c+d)^3
(2+x)^3
(x+1)^3
(a+3b)^3
(2+5a)^3
(3+5a)^3
(2+a)^3
(x+y)^3
(1+4a)^3
к 5 формуле:
(n-q)^3
(c-d)^3
(2-x)^3
(x-1)^3
(a-3b)^3
(2-5a)^3
(3-5a)^3
(2-a)^3
(x-y)^3
(1-4a)^3
к 6 формуле:
x^3+y^3
x^3+8
c^3+27
x^3+27y^3
27x^3+8y^3
x^3+y^3
64+25t^3
343+8b^3
y^3+125
216+27z^3
к 7 формуле:
x^3-y^3
x^3-8
c^3-27
x^3-27y^3
27x^3-8y^3
x^3-y^3
64-25t^3
343-8b^3
y^3-125
216-27z^3
одз подкоренное выражение x² - x - 20 ≥ 0
D=1 + 80 = 81
x12=(1+-9)/2 = -4 5
[-4] [5]
x∈(-∞ -4] U [5 +∞)
(х+2)√(х²-х-20) = 6х+12
(х+2)√(х²-х-20) = 6(х+2)
x=-2 не является корнем так как не проходит по ОДЗ значит можно разделить на х+2
√(х²-х-20) = 6
возводим в квадрат
х²-х-20 = 36
х²-х-56 = 0
D= 1 - 4 * 1* (-56) = 225 = 15²
x12=(1 +-15)/2 = - 7 8
x1=-7 проходит по ОДЗ
х2=8 проходит по одз
ответ {-7, 8}