Теплоход проходит по течению реки до пункта назначения 352 км и после стоянки возврашается в пункт отправления.найдите скорость теплохода в неподвижной воде,если скорость течения равна 3 км/ч,стоянка длится 6
часов, в пункт отправления теплоход возврашается через 44 часа после отплытия из него.ответ дайте в км\ч
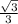 ;
;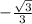 ;
;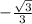 и
и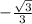 ;
;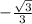 );
);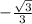 );
);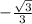 )+2kπ, k∈Z;
)+2kπ, k∈Z;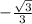 )+2kπ, k∈Z;
)+2kπ, k∈Z;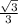 )+2kπ, k∈Z
)+2kπ, k∈Z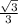 )+π-2kπ, k∈Z;
)+π-2kπ, k∈Z;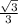 )+2kπ, k∈Z
)+2kπ, k∈Z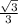 )+π+2kπ, k∈Z;
)+π+2kπ, k∈Z;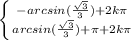 , k∈Z
, k∈Z
x - скорость теплохода в неподвижной воде,
х+3 - скорость теплохода по течению реки,
х-3 - скорость теплохода против течению реки,
352/(х+3) - время движения по течению реки,
352/(х-3) - время движения против течению реки,
352/(х+3) + 352/(х-3) + 6 = 44,
352/(х+3)+352/(х-3)-38=0,
352(x-3)+352(x+3)-38(x+3)(x-3)=0,
352x-1056+352x+1056-38x^2+342=0,
-38x^2+704x+342=0,
19x^2-352x-171=0,
D1=176^2+19*171=30976+3249=34225,
sqrt(D1)=sqrt(34225)=185,
x1=(176-185)/19=-9/19 <0 - не соответствует условию задачи,
x2=(176+185)/19=19.
ответ: 19 км/ч