1) (3x+0,5)^2
(3х+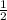 )^2
)^2
9х^2+3х+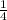
2) (-4x+7y) (-4x+7y)^2
(7у-4х)^2
49у^2-56ху+16х^2
3) (x^2+y^3)^2
(х^2)^2+2х^2y^3+(y^3)^2
x^4+2x^2y^3+y^6
Напишем формулу для суммы 9 членов геометрической прогрессии
s9=(b1*(q^9-1))/(q-1)
Напишем формулу для суммы 18 членов геометрической прогрессии
s18=(b1*(q^18-1))/(q-1)
512=2^9
s9/(s18-s9)=2^9
GПеревернем дробь
(s18-s9)/s9=1/2^9
Числитель разделим на знаменатель почленно.
1-s18/s9=1/2^9 Отдельно упростим дробь s18/s9
s18/s9=(b1*(q18-1)/(q-1))/(b1*(q9-1)/(q-1)
Сократятся b1 и (q-1)
s18/s9=(q18-1)/(q9-1) разность квадратов
s18/s9=((q:9-1)*(q^9+1))/(q9-1) Сократим на (q^9-1)
s18/s9=q^9+1
Возвращаемся к уравнению
1-s18/s9=1/2^9
1-q^9+1=1/2^9
-q^9=1/2^9
q=-1/2
1) 9x^2+3x+2.5
2)16x^2-56xy+49y^2
3) x^4+2x^2y^3+y^6