вспомним что такое модуль
|x| = x x>=0
= -x x<0
Пишем на всякий случай ОДЗ x≠3 и смотрим подмодульное выражение
(x²+x-2)/(x-3) = (x+2)(x-1)/(x-3)
D=1+8 = 9
x12=(-1+-3)/2 = -2 1
смотрим метод интервалов
[-2] [1] (3)
Итак при
1. x∈[-2 1) U (3 + ∞)
|(x²+x-2)/(x-3)| = (x²+x-2)/(x-3)
2. x∈(-∞-2) U [1 3)
|(x²+x-2)/(x-3)| = - (x²+x-2)/(x-3)
решаем полученные уравнения
1. x∈[-2 1] U (3 + ∞)
(x²+x-2)/(x-3) = (x²+x-2)/(x-3) решения все числа на интервалах с учетом одз
x∈[-2 1) U (3 + ∞)
2. x∈(-∞-2) U (1 3)
(x²+x-2)/(x-3) = - (x²+x-2)/(x-3)
2(x²+x-2)/(x-3) = 0
x=1 x=-2 решений нет
ответ x∈[-2 1] U (3 + ∞)
1) h =13m; 2) t =1+ √1,3+
Объяснение:
h = 18t - 5t²
вначале при полете вверх на камень действует сила тяжести, которая снижает его скорость до полной остановки, а затем он под действием силы тяжести вернется обратно на землю.
1) определим в какой момент времени камень брошенный вверх потеряет скорость (v=0)
v = v0 - gt ; v0-gt = 0
t = v0/g время подъема, t = 10/10 =1 c.
а теперь рассчитаем высоту на которую он поднимется
h = 18v0/g - 5(v0/g)² (для удобства расчета примем g=10)
h = 18*10/10 - 5(10/10)² =18 - 5 =13
h =13 m t = 1 время подъема
2)теперь определим время возврата мяча на землю под действием силы тяжести.
h = v0t + gt²; где v0=0 начальная скорость. g =10
h = gt²
t² = h/g
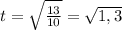 время падения
время падения
полное время полета с момента запуска
t = t1 + t2 = 1 + √1.3
2) 6/к3 | *к3 = 6к3/3 = 2к3, 5/к5 | *k5 = 5k5/5 = k5. 11/k22 | k22 = 11k22/k22 = k2/2
к-корень