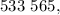 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).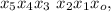


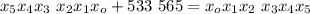 ;
;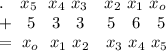

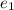 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого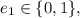
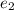 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго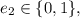
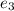 – возможная добавочная единица,
– возможная добавочная единица,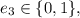
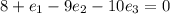 ;
;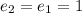 и при
и при  ;
;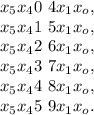
 поскольку
поскольку 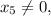 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.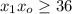 .
.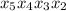 .
.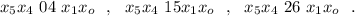
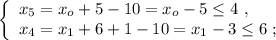

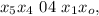
 может играть роль апреля.
может играть роль апреля.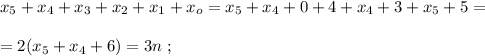
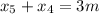 ;
;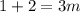 ;
;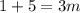 ;
;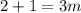 ;
; ;
;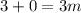 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.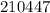 – дата 21/04/47 г.
– дата 21/04/47 г.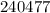 – дата 24/04/77 г.
– дата 24/04/77 г.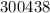 – дата 24/04/38 г.
– дата 24/04/38 г.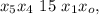
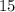 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;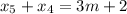 ;
;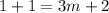 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

2^(x-1) -2^(x-6) > 17 ;
(2^(x-6) ) *(2^5 -1) >17 ;
2^(x-6) > 17/31 ;
x-6 > Log_2 17/31 ;
x > 6 + Log_2 17/31 иначе x∈( 6 + Log_2 17/31 ;∞) .
---
было бы лучше :
2^(x-1) +2^(x-5) > 17 ;
(2^(x-5))*(2⁴+1) >17
2^(x-5) > 1 ;
2^(x-5) > 2⁰ ;
x-5 > 0 ⇒ x >5 иначе x∈(5 ;∞).
2.
5^(3x) +3*5^(3x-2) < 140 ;
5^(3x-2) * (5² +3) < 140 ;
5^(3x-2) < 5 ;
3x-2 <1 ⇒ x <1 иначе x∈(-∞ ; 1).
ответ : x∈( - ∞ ;1).
3.
3^(x+2)+3^(x-1) ≤28 ;
3^(x-1)* (3³+1) ≤ 28 ;
3^(x-1)*28 ≤ 28 ;
3^(x-1) ≤ 1 ;
3^(x-1) ≤ 3⁰ ;
x-1 ≤ 0 ;
x ≤ 1 иначе x∈ (-∞ ; 1].
ответ : x∈( - ∞ ;1].