2) как известно все углы прямоугольника прямые. <А=<В=<С=<D=90`
С диагоналей разбивает их на прямоугольные треугольники ACD и АВС .
угол ACD равен 60' по условии задачи . А угол D =90' => угол CAD=30'. Итак все углы треугольника АСD известны теперь переходим на треугольник АВО. Т .к. угол А =90' в угол САD=30' угол ВАО=60' . Угол ВЕА =90' в угол BAO=60' значит угол ABE=30'=ЕВО.
По условии задачи ОЕ=4см . По условии прямоугольного треугольника :если один из углов треугольника равен 30' то противоположный катет равен половине гипотенузы. В нашем случае катет лежащий противоположно углу ЕВО=30' это ОЕ=4см
Отсюда следует что гипотенуза ВО=2ОЕ=2×4=8 . Так как точка О середина отрезка BD то ВD=2 ×BO=2×8=16
B прямоугольника диагонали равны значит диагональ АС=ВD= 16 см
Объяснение:
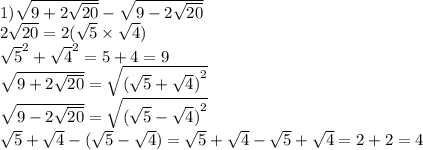
2) как известно все углы прямоугольника прямые. <А=<В=<С=<D=90`
С диагоналей разбивает их на прямоугольные треугольники ACD и АВС .
угол ACD равен 60' по условии задачи . А угол D =90' => угол CAD=30'. Итак все углы треугольника АСD известны теперь переходим на треугольник АВО. Т .к. угол А =90' в угол САD=30' угол ВАО=60' . Угол ВЕА =90' в угол BAO=60' значит угол ABE=30'=ЕВО.
По условии задачи ОЕ=4см . По условии прямоугольного треугольника :если один из углов треугольника равен 30' то противоположный катет равен половине гипотенузы. В нашем случае катет лежащий противоположно углу ЕВО=30' это ОЕ=4см
Отсюда следует что гипотенуза ВО=2ОЕ=2×4=8 . Так как точка О середина отрезка BD то ВD=2 ×BO=2×8=16
B прямоугольника диагонали равны значит диагональ АС=ВD= 16 см
Объяснение:
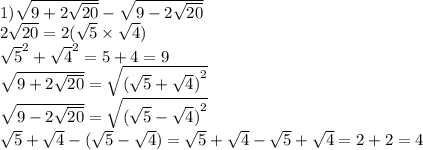
1) 220/128 + 350/256 = 220/128 + 175/128 = 395/128 = 3 11/128
2) 300/15 + 691/4 = 20 + 170 + 11/4 = 192 3/4
3) 111/40 + 561/6 = 2 31/40 + 93 3/6 = 95 31/40 + 20/40 = 95 51/40 = 96 11/40
4) 35/38 + 83/81 = (35*81+38*83)/(38*81) = 5989/3078 = 1 2911/3078