Сначала построим график функции, которая под модулем. Что делает модуль? Он все отрицательные ЗНАЧЕНИЯ делает положительными, то есть получив график функции нам надо будет всё что ниже оси Ох поднять наверх (отразить относительно оси Ох).
И так надо построить этот график. Это парабола, ветви которой вверх, координаты вершины (1/3;-4/3). И найдём точки пересечения с осями координат:
Можем строить.
И так надо отразить относительно оси Ох значения функции f(x) на интервале от -1/3 до 1. Получилась нужная нам функция, её можно записать как:
И естественно так как мы отразили относительно оси Ох, то значения вершины и точка пересечения с осью Оу.
Пусть l метров в час - скорость бурения 3 скважины, а t - время, через которое её глубина стала равной глубине второй скважины. Так как последняя равна 1*t=t метров в час, то получаем уравнение l*(t-1)=t. По условию, l*(t-1+1,5)=l*(t+0,5)=2*(t+1,5). Из первого уравнения находим l=t/(t-1). Подставляя это выражение во второе уравнение, получаем уравнение t(t+0,5)/(t-1)=(t²+0,5*t)/(t-1)=2t+3, или t²+0,5*t=(2t+3)(t-1), или t²+0,5*t=2t²+t-3, или t²+0,5t-3=0, или 2t²+t-6=0. Дискриминант D=1²-4*2*(-6)=49=7². Отсюда t=(-1+7)/4=1,5 часа, а l=t/(t-1)=1,5/0,5=3 метра в час. ответ: 3 метра в час.
Арифметическая прогрессия - это последовательность, у которой каждое последующее число получается из предыдущего добавлением к нему постоянного числа d, называемого шагом или разностью. Шаг м.б. как положительным, так и отрицательным числом. 1) Проверим, будет ли постоянным шаг, если из n-го члена последовательности вычесть (n-1)-й член. n-й член нам дан: an = 5n + 3, найдём (n-1)-й: a(n-1) = 5 (n - 1) + 3 = 5n -2. Вычитаем, an - a(n-1) = 5n + 3 - 5n + 2 = 5 = d Получили постоянную, которая не зависит от n, значит, это арифметическая прогрессиия, d = 5. Считаем сумму 10 первых членов по формуле: Sn = (1/2) * (2*a1 + d*(n - 1)) * n Для этого надо знать ещё a1 = 5 *1 + 3 = 8 S10 = (1/2) * (2*8 + 5*(10-1))*10= (16 + 45)*5 = 305
Сначала построим график функции, которая под модулем. Что делает модуль? Он все отрицательные ЗНАЧЕНИЯ делает положительными, то есть получив график функции нам надо будет всё что ниже оси Ох поднять наверх (отразить относительно оси Ох).
И так надо построить этот график. Это парабола, ветви которой вверх, координаты вершины (1/3;-4/3). И найдём точки пересечения с осями координат: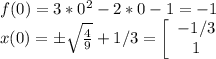
Можем строить.
И так надо отразить относительно оси Ох значения функции f(x) на интервале от -1/3 до 1. Получилась нужная нам функция, её можно записать как:
И естественно так как мы отразили относительно оси Ох, то значения вершины и точка пересечения с осью Оу.