2) f(2)=6, f(-3)= -14
2) f(x)= -x² +3x+4
f(2)= - 2²+3*2+4= - 4+10=6
f(-3)= -(-3)²+3*(-3)+4= -9 -9+4= -14
3) f(x)=2х²+3х-3
-это график параболы, ветви направлены вверх, она в два раза уже параболы у=х², опущена на 3 единицы вниз по оси ОУ
f'(x)=(2х²+3х-3)'= 4x+3 -производная
4х+3=0
4х=-3
х= - 3/4 ( абсцисса вершины)
теперь чертишь прямую с этой точкой ( точка чёрная закрашенная)
-3/4
----------------------------------.---------------------------------------→Х
- +
f(x) убывает на х ∈ ( -∞; -3/4]
f(x) возрастает на х ∈ [-3/4; +∞)
f(-3/4)= (-3/4)²+3*(-3/4)-4= 9/16- 9/4 - 4=9/16-36/16-4=
2) f(2)=6, f(-3)= -14
2) f(x)= -x² +3x+4
f(2)= - 2²+3*2+4= - 4+10=6
f(-3)= -(-3)²+3*(-3)+4= -9 -9+4= -14
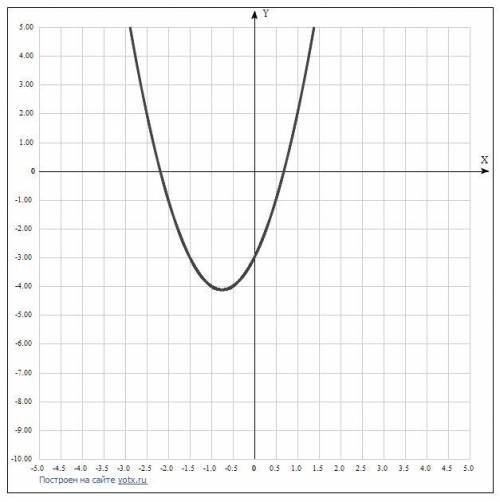
3) f(x)=2х²+3х-3
-это график параболы, ветви направлены вверх, она в два раза уже параболы у=х², опущена на 3 единицы вниз по оси ОУ
f'(x)=(2х²+3х-3)'= 4x+3 -производная
4х+3=0
4х=-3
х= - 3/4 ( абсцисса вершины)
теперь чертишь прямую с этой точкой ( точка чёрная закрашенная)
-3/4
----------------------------------.---------------------------------------→Х
- +
f(x) убывает на х ∈ ( -∞; -3/4]
f(x) возрастает на х ∈ [-3/4; +∞)
f(-3/4)= (-3/4)²+3*(-3/4)-4= 9/16- 9/4 - 4=9/16-36/16-4=

подводим log под одно основание
log3(x^2-2x)>log3 3
потом отбрасываем log
x^2-2x>3
x^2-2x-3>0
x=-1, x=3
ОДЗ: x^2-2x>0
x(x-2)>0
x=(-бесконечность;0) () (2;+ бесконечность)
ответ: x= (-бесконечность;-1) () (3;+ бесконечность)