y=1/3x+13/3
Объяснение:
Чтобы составить уравнение прямой по двум точкам, нужно знать формулу. Для этого обозначим X1 - абсцисса первой точки, X2 -абсцисса второй, Y1 -ордината первой, Y2- ордината второй.
Тогда уравнение прямой, проходящей через точки с этими координатами будет иметь вид:
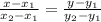 Подставим числа
Подставим числа
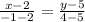
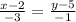 Воспользуемся свойством пропорции, предварительно умножив обе части равенста на минус единицу.
Воспользуемся свойством пропорции, предварительно умножив обе части равенста на минус единицу.
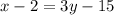 . Оставим игрик в правой части,а все остальное перенесем влево, тогда
. Оставим игрик в правой части,а все остальное перенесем влево, тогда
3y=x+13 Разделим обе части равенства на 3
y=1/3x+13/3
Точки с координатами (-2;8) и (1;5)
Объяснение:
Первая функция
у= х²+4 (1)
Выразим у во второй функции:
х+у = 6 <=> у = 6-х (2)
Точка пересечения - точка, с некими координатами (х0;у0), которые принадлежат обоим графикам функций.
То есть нам надо найти такие х и у, для которых верно равенство 1 и 2.
Приравняем у в (1) и (2) функциях. Получим:
у = х²+4 = 6-х
Или
Найдем у для х=(-2) и х=1
Для этого подставим значение х в любую из 2х функций
При х = (-2)
у(-2) = 6-(-2) = 6+2 = 8
Следовательно одна из искомых точек имеет координаты:
(-2;8)
При х=1
у(1) = 6-1 = 5
Следовательно вьорая искомая точек имеет координаты:
(1;5)
ответ: (-2;8) и (1;5)