Формула площади прямоугольного треугольника:
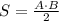 ,
,
где А и В - его катеты.
Обозначим наибольший катет за Х, меньший за Х-5.
Получим уравнение:
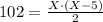 ,
,
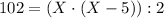 ,
,
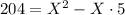 ,
,
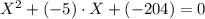 или
или
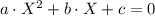 .
.
Есть несколько вариантов пути решения. Мы выбираем самый простой, но длинный - через дискриминант.
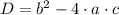 ,
,
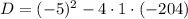 ,
,
D = 25 + 816 = 841
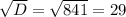
Получаем два корня квадратного уравнения:
1 корень
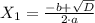 ,
,
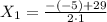 ,
,
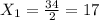 см,
см,
Это то, что нужно.
2 корень
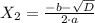 ,
,
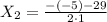 ,
,
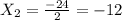 .
.
Полученное значение геометрического смысла не имеет, ну не может сторона треугольника на чертеже быть с отрицательной длиной.
Большую сторону нашли. Найдем меньшую:
17 - 5 = 12 см
Проверим полученный результат:
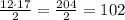
ответ: 12, 17 катеты прямоугольного треугольника, площадь которого 102 см2.
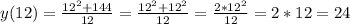
(2a)*(7b) и 14ab
(-2a)*(2a) и 0
3(a+b) и 3ab
12(a-b) и 12a-12b