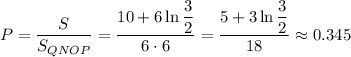15 ! два действительных числа случайным образом выбираются из отрезка [0,6]. какова вероятность того, что сумма двух чисел меньше 5, а их произведение меньше 6? решать с определения вероятности
Расписываем (x-2)^2 по формуле сокращенного умножения (a-b)^2=a^2-2ab+b^2 получаем (x^2-4x+4)/(x-1)<0 решаем квадратное уравнение x^2-4x+4=0 D=0, значит -b/2a и один корень x=2 :> a(x-x1)(x-x1)(x-2)(x-2) это у нас такая формула есть (не знаю как она называется) значит общая у нас будет (x-2)(x-2)/(x-1)<0 у нас неравенство, значит x=2 x=1 пишем это на линию ___+1-2+> считаем интервалы + и - нам нужно меньше нуля , значит от 1 до 2 ответ : "(1;2)" (скобки не квадратные потому что у нас не меньше либо равно 0, а просто меньше нуля)
1) S=(a²√3)/4=16√3 a²=64, a=8 - сторона треугольника основания, т.к. две боковые грани ⊥ плоскости основания, значит пересечение боковых граней ⊥ основанию, т.е. это пересечение - высота пирамиды. Другая грань наклонена под ∠45° к пл-сти основания, значит две другие грани равнобедренные прямоугольные Δ, с катетами =8. Их площади =(8*8)/2+(8*8)/2=64. Найдем длину двух боковых ребер: с²=8²+8²=2*8², с=√(2*8²)=8√2. Боковые ребра: 8, 8√2, 8√2 Найдем апофему боковой грани: h²+4²=128, h=√( 128 -16)=√112=√16*7=4√7, Площадь этой грани =(8*4√7)/2=16√7 Площадь боковой поверхности=64+16√7
Пусть х - первое число, у - второе число. По условию,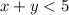 откуда
откуда 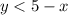 и
и 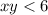 откуда
откуда 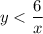
Найдем точки пересечения графиков функций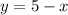 и
и 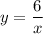 . Для этого приравниваем функции
. Для этого приравниваем функции
По теореме Виета
Смотрим рисунок. Разобьем заштрихованную фигуру прямыми x = 2 и x = 3 и найдем площади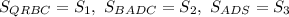
Площадь заштрихованной фигуры: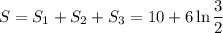
Искомая вероятность: