logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
kutirev123p
kutirev123p
31.01.2022 00:18 •  Алгебра

Найдите среднюю линию трапеции если сумма двух оснований равна 24см​

👇
Увидеть ответ
Ответ:
фыыыы1
фыыыы1
31.01.2022

Средняя линия трапеции равна полусумму двух оснований.  

24/2=12 см.

Объяснение:

4,5(17 оценок)
Ответ:
nastiasteinoxz34d
nastiasteinoxz34d
31.01.2022

Средняя линия трапеции параллельна основам и равна их полусумме.

Поэтому средняя линия данной трапеции равна

24:2=12см

ответ: 12см средняя линия трапеции

4,8(63 оценок)
Открыть все ответы
Ответ:
polka3893
polka3893
31.01.2022
Найти неопределенные интегралы. Результаты проверить
дифференцированием.
а) ∫(3x^2+4/x+cosx+1)dx=x³+4·ln IxI+sinx +x +C 
проверка:
(x³+4·ln IxI+sinx +x +C)'=3x²+4/x +cosx+1  -  верно

б) ∫[4x/√(x^2+4)]dx=    [ (x^2+4)=t     dt=2xdx ]   =∫2dt/√t=4√t+c=4√(x^2+4)+c
проверка:
(4√(x^2+4)+c)'=[4(1/2)/√(x^2+4)]·2·x =4x/√(x^2+4)  -  верно

в) ∫-2xe^xdx  =-2 ∫xe^xdx= [ x=u         e^xdx=dv  ]
                                           [ dx=du       e^x=v      ]

-2 ∫xe^xdx=-2( u·v- ∫vdu)=-2(x·e^x-∫e^x·dx)=-2(x· e^x-e^x)+c=-2·(e^x)·(x-1)+c
проверка:
(-2·(e^x)·(x-1)+c)'=-2((e^x)'·(x-1)+(e^x)·(x-1)')=-2((e^x)·(x-1)+(e^x))=-2(e^x)·x
=-2x·(e^x) - верно
4,5(25 оценок)
Ответ:
dashasapleva6
dashasapleva6
31.01.2022

Найдём координаты вектора 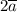2 \overline a. Для этого все координаты вектора 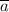\overline a нужно умножить на 2:

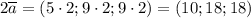
2 \overline a =(5 \cdot 2; 9 \cdot 2; 9 \cdot 2)=(10;18;18)

По такому же принципу найдём координаты вектора 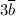3 \overline b:

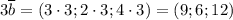
3 \overline b = (3 \cdot 3; 2 \cdot 3; 4 \cdot 3)=(9;6;12)

Чтобы найти координаты вектора 2 \overline a - 3 \overline b, вычтем соответствующие координаты:

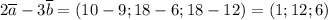
2 \overline a - 3 \overline b = (10-9; 18-6; 18-12)=(1;12;6)

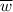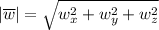Длина произвольного вектора \overline w вычисляется по формуле | \overline w|=\sqrt{w_x^2+w_y^2+w_z^2} :

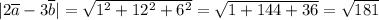
|2 \overline a - 3 \overline b |=\sqrt{1^2+12^2+6^2}=\sqrt{1+144+36}=\sqrt{181}

ответ: 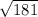\sqrt{181}.

***

Координаты середины отрезка есть среднее арифметическое координат конца отрезка:

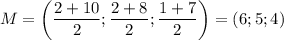
M=\left(\dfrac{2+10}{2}; \dfrac{2+8}{2}; \dfrac{1+7}{2}\right)=(6;5;4)

***

По условию точка 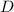D делит сторону 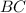BC пополам (и так же с двумя другими точками). Найдём координаты точки

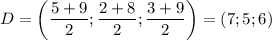
D=\left(\dfrac{5+9}{2}; \dfrac{2+8}{2}; \dfrac{3+9}{2}\right)=(7;5;6)

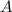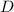Расстояние между точками A и D (т. е. длина медианы) равно:

\sqrt{(3-7)^2+(2-5)^2+(5-6)^2}=\sqrt{16+9+1}=\sqrt{26}

То есть AD=\sqrt{26}.

То же самое проделаем с двумя другими медианами:

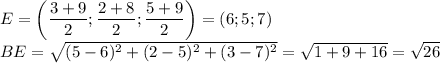
E=\left(\dfrac{3+9}{2}; \dfrac{2+8}{2};\dfrac{5+9}{2}\right)=(6;5;7)\\BE=\sqrt{(5-6)^2+(2-5)^2+(3-7)^2}=\sqrt{1+9+16}=\sqrt{26}

- - - - - - -

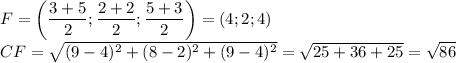
F=\left(\dfrac{3+5}{2};\dfrac{2+2}{2};\dfrac{5+3}{2}\right)=(4;2;4)\\CF=\sqrt{(9-4)^2+(8-2)^2+(9-4)^2}=\sqrt{25+36+25}=\sqrt{86}

***

Если что-либо будет непонятно — спрашивайте.

4,8(67 оценок)
Это интересно:
П
Как измерить температуру у лошади: советы от опытных ветеринаров и коневодов...
Д
Дом-и-сад
22.09.2020
Как удалить пятна от кондиционера для белья: советы экспертов...
З
Здоровье
05.02.2023
Как сдержать газы: 7 важных советов...
Д
Дом-и-сад
10.09.2020
Заставьте ваш филодендрон расцвести: советы по уходу за растением...
В
Как определить, что девушка пытается увести вашего парня...
К
Как приготовить вкусное мороженое из молока в домашних условиях...
К
Как правильно ответить на сообщение?...
К
Лучший способ приготовления традиционных макарон с сыром...
С
Хна для волос: как правильно сочетать и наносить?...
З
Здоровье
25.04.2020
Как вывести токсины из легких с помощью натуральных средств...
Новые ответы от MOGZ: Алгебра
Arcator
Arcator
10.02.2021
Задайте формулой сложную функцию: g(x) = f(x+4), если f(x) = (x-2)/x^2...
Математик094
Сколько решений имеет система уравнений x-y=1 3x-3y=-9?...
iltubaevapg
iltubaevapg
13.01.2020
Найди значение выражения 4(k−15)−t(15−k), если k=2, t=6....
Ди1501
Ди1501
27.04.2021
Дано многочлен -х+3х-5.Чему равна его степень.​...
Olya199701
Olya199701
07.12.2021
2x(x+23)2−x2(x+23)=0. 3 корня По возрастанию...
анр5гн5р5рррр
Решите уравнение (4 – x) (х + 4) + x2 = 4 — x онлайн мектеп с решением​...
MGap58
MGap58
15.12.2022
Найдите первый член прогрессии an в которой q=-20, s1=330...
pourkur1111oz10kt
pourkur1111oz10kt
15.12.2022
А) 2x-5/x+5 - 4 = 0 б) 12/7-х = х в) х^2-4/4 = 3+2х/2 г) 10/2х-3 = х-1...
марго170
марго170
15.12.2022
1. (2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^+6y 2. (a-1)(a^2+1)(a^4-a^2+1)(a^6-1)...
angelinasd2007
angelinasd2007
06.08.2021
Что должно быть в квадрате чтоб получить 12?...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ