1. -1,4
2. Одночленом не является то выражение, части которого не разделяются плюсом или минусом (К примеру, 2abc будет одночленом, а ab + 2c не будет, в общем, ab + 2c будет многочленом), в данном случае ответом будет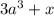 
3. Подобные слагаемые - те, которые имеют одну и ту же буквенную часть (Если одна буква возведена в одну степень, а другая в другую, они не будут подобными слагаемыми), при выполнении действий с ними, коэффициенты (Числа перед буквами) слагаются/вычисляются, в данном случае ответом будет 3a + 4b
4. При умножении одинаковых переменных степени слагаются, т.е., в данном случае будет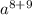 
= 
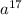
5. 
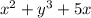, как решать, я уже объяснял
6. 4y + 5 (8y - (4y - 5) = 8y - 4y + 5, так как перед скобкой стоит минус, остальное я уже объяснял)
7. 16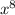
, так как, если после скобок стоит степень, степени внутри скобок умножаются на степень после скобок
8. 12x - 14 (Просто число перед скобками умножается на числа внутри скобок)
9. 
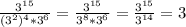(В конце степени просто сокращаются, и остается только 3)
10. 
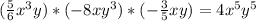(Коэффициенты сокращаются, и в итоге остается 
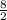, что равно 4, а результат положительный, так как отрицательное число, умноженное на отрицательное, становится положительным)
x=3 x=-1 x=-4
_ + _ +
(-4)(-1)(3)
x∈(-∞;-4) U (-1;3)
2. 1/3 x^3 - 3х <= 0
1/3x(x²-9)≤0
1/3x(x-3)(x+3)≤0
x=0 x=3 x=-3
_ + _ +
[-3][0][3]
x∈(-∞;-3] U [0;3]
3. (x^2+6x+9) (x^2-1) <= 0
(x+3)²(x-1)(x+1)≤0
x=-3 x=1 x=-1
+ + _ +
[-3][-1][1]
x∈[-1;1] U {-3}
4. (x+2) (x-3) (x-4) / (x-2)^2 > 0
x=-2 x=3 x=4 x=2
_ + + _ +
(-2)(2)(3)(4)
x∈(-2;2) U (2;3) U (4;∞)
5. (x^2-x+3) (6x+1)^5 > 0
x²-x+3=0
D=1-12=-11<0⇒x²-x+3>0 при любом х⇒(6x+1)^5>0
6x+1>0⇒6x>-1⇒x>-1/6
x∈(-1/6;∞)
6. (3x-1) (x-2) (x+1) > 0
x=1/3 x=2 x=-1
_ + _ +
(-1)(1/3)(2)
x∈(-1;1/3) U (2;∞)
7. (x^2-7x+12) (x^2-4) >= 0
x²-7x+12=0⇒x1+x2=7 U x1*x2=12⇒x1=3 U x2=4
x²-4=0⇒x²=4⇒x=-2 U x=2
+ _ + _ +
[-2][2][3][4]
x∈(-∞;-2] U [2;3] U [4;∞)
8.( 9x^2+12x+4) / (x-6 )>= 0
(3x+2)²(x-6)≤0
x=-2/3 x=6
_ _ +
[2/3][6]
x∈[6;∞) U {2/3}
9. (x-3)^10 (x-1)^9 x^4(x+2)<=0
x=3 x=1 x=0 x=-2
+ _ _ + +
[-2][0][1][3]
x∈[-2;1] U {3}
10.( x^4-8x^2-9) / (x^3-1) <0
x^4-8x²-9=0
x²=a
a²-8a-9=0⇒a1+a2=8 U a1*a2=-9⇒a1=-1 U a2=9
(x²+1)(x²-9)/(x³-1)<0
(x²+1)(x-3)(x+3)/(x-1)(x²+x+1)<0
x²+1>0 при любом х и x²+x+1>0 при любом х⇒
(x-3)(x+3)/(x-1)<0
x=3 x=-3 x=1
_ + _ +
(-3)(1)(3)
x∈(-∞;-3) U (1;3)