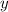сторону катета образованного боковой стороной квадрата относительно ее основанию, за 
сторону квадрата , она же сторона отсеченной боковой стороны треугольника (выше большего основания) . 
. 
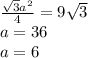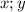удовлетворяет ему такое условие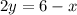 
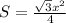, и остались два маленьких прямоугольных треугольника их площади равны в сумме 
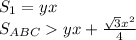тогда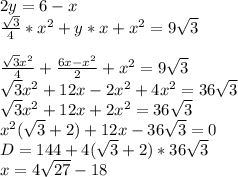 
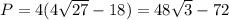
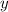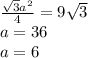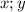сторону катета образованного боковой стороной квадрата относительно ее основанию, за сторону квадрата , она же сторона отсеченной боковой стороны треугольника (выше большего основания) . . удовлетворяет ему такое условие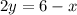 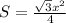, и остались два маленьких прямоугольных треугольника их площади равны в сумме 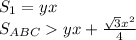тогда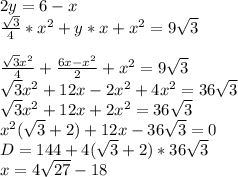 
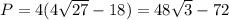
Sunny plain — солнечная равнина
Extensive desert Обширная пустыня
Vast, flat prarie — Обширная плоская прерия
Deep canyon — глубокий каньон
Huge mountain range — огромный горный хребет
High mountain — высокая гора
Heavy forests - густые леса