Продолжительность импульсной фазы солнечных вспышек обычно не превышает нескольких минут, а количество энергии, высвобождаемой за это время, может достигать миллиардов мегатонн в тротиловом эквиваленте. Энергию вспышки традиционно определяют в видимом диапазоне электромагнитных волн по произведению площади свечения в линии излучения водорода Нα, характеризующей нагрев нижней хромосферы, на яркость этого свечения, связанную с мощностью источника.
В последние годы часто используют также классификацию, основанную на патрульных однородных измерениях на серии ИСЗ, главным образом GOES[1], амплитуды теплового рентгеновского всплеска в диапазоне энергий 0,5—10 кэВ (с длиной волны 0,5—8 ангстрем). Классификация была предложена в 1970 году Д.Бейкером и первоначально основывалась на измерениях спутников «Solrad»[2]. По этой классификации солнечной вспышке присваивается балл — обозначение из латинской буквы и индекса за ней. Буквой может быть A, B, C, M или X в зависимости от величины достигнутого вспышкой пика интенсивности рентгеновского излучения[3][Комм 1]:
БукваИнтенсивность в пике (Вт/м2)Aменьше 10−7Bот 1,0×10−7 до 10−6Cот 1,0×10−6 до 10−5Mот 1,0×10−5 до 10−4Xбольше 10−4
Солнечная вспышка 14 декабря 2014 года: выброс отрывается от поверхности.
Индекс уточняет значение интенсивности вспышки и может быть от 1,0 до 9,9 для букв A, B, C, M и более — для буквы X. Так, например, вспышка 12 февраля 2010 года балла M8.3 соответствует пиковой интенсивности 8,3×10−5 Вт/м2. Самой мощной (по состоянию на 2010 год) зарегистрированной с 1976 года[4] вспышке, произошедшей 4 ноября 2003 года, был присвоен балл X28[5], таким образом, интенсивность её рентгеновского излучения в пике составляла 28×10−4 Вт/м2. Следует заметить, что регистрация рентгеновского излучения Солнца, так как оно полностью поглощается атмосферой Земли, стала возможной начиная с первого запуска космического аппарата «Спутник-2» с соответствующей аппаратурой[6], поэтому данные об интенсивности рентгеновского излучения солнечных вспышек до 1957 года полностью отсутствуют.
Измерения в разных диапазонах длин волн отражают разные процессы во вспышках. Поэтому корреляция между двумя индексами вспышечной активности существует только в статистическом смысле, так для отдельных событий один индекс может быть высоким, а второй низким и наоборот.
Солнечные вспышки, как правило, происходят в местах взаимодействия солнечных пятен противоположной магнитной полярности или, более точно, вблизи нейтральной линии магнитного поля, разделяющей области северной и южной полярности. Частота и мощность солнечных вспышек зависят от фазы 11-летнего солнечного цикла.
12.14
Функциональная схема (программа):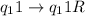
, 
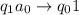
12.17
смотри объяснение
Объяснение:
12.14
Алфавит внутренних состояний Q = {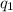
, 
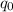} — рабочее состояние и остановка соответственно.
Начальное положение — над первым символом слова.
Будем последовательно считывать символы на ленте, двигаясь по ней слева направо. Если считали 1, просто переходим в соседнюю ячейку:
Если считали пустой символ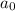
, то мы попали в ячейку сразу после ячейки с последним символом заданного слова. Заменяем этот пустой символ на единицу и останавливаемся:
Построили машину Тьюринга, которая слово вида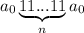
преобразовывает в слово вида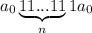 
12.17
Внешний алфавит A = {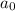
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0} — пустой символ и все цифры десятичной системы счисления.
Алфавит внутренних состояний Q = {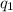
, 
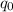} — рабочее состояние и остановка соответственно.
Функциональная схема (программа):
Начальное положение — над последним символом слова на входе (как написано в тексте на скриншоте, стандартное положение).
Пояснение к работе построенной машины. Если отнимание единицы из последней цифры не требует перехода 10-ти из разряда слева, то просто вычитаем и останавливаемся (первая команда). Но если последняя цифра — ноль, то после замены его на 9 придется перейти к символу слева (вторая команда) и с ним повторить все те же действия, что и с последним символом. И так до тех пор, пока не встретим символ, отнимание единицы из которого не требует перехода 10-ти из разряда слева. Короче говоря, все как при обычном вычитании в столбик. Последние три команды убирают (заменяют на пустые символы) ведущие нули, если они, конечно, появились.