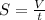logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
BelkaNext
BelkaNext
23.12.2021 14:23 •  Другие предметы

Кто такой Эзоп? 1) собиратель фольклора 2) древнегреческий баснописец

👇
Увидеть ответ
Ответ:
hatasa75
hatasa75
23.12.2021
(A-B):3 (км/ч) - с такой скоростью нужно ехать поезду
4,7(89 оценок)
Открыть все ответы
Ответ:
OlgaStarikova
OlgaStarikova
23.12.2021
Пусть колесо, буксуя,  катится вправо и центр колеса перемещается со скоростью u по модулю.  Перейдем в систему отсчета, движущую с этой скоростью тоже вправо. В этой системе центр колеса неподвижен, а верхняя и нижняя точки колеса имеют одинаковую по модулю скорость. Как преобразуется скорость при переходе в подвижную систему, видно на примере придорожного столба.  Он движется назад, влево, со скоростью u. Наблюдатель в подвижной системе не только столбу, но и всем  точкам «приписывает» вектор скорости, равный по модулю  u  и направленный влево. Это значит, что модуль скорости верхней точке в подвижной ситеме меньше, чем в неподвижно, а для нижней точки наоборот. То есть имеет место уравнение V2-u=V1+u ⇒ u=(V2-V1)/2=4 м/с
4,8(96 оценок)
Ответ:
эмка89
эмка89
23.12.2021
                                                    Решение:
В задаче сказано, что всадник проехал 80 км за 5 часов, тогда узнаем с какой скоростью он проехал это расстояние.Для этого воспользуемся формулой нахождение скорости:
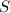S= \frac{V}{t} , где S -расстояние которое проехал всадник, а 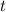t  - час,за который было пройденное расстояние.
                                                  S=80 км;
                                                   t=5 ч;
                                Подставим данные у формулу:
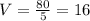                                V= \frac{80}{5}=16  км/ч;
Получается что всадник проехал 80 км, со скоростью 16 км/ч. Найдем сколько времени потратил на путь мотоциклист, но сначала узнаем его скорость. В условии задаче сказано, что скорость мотоциклиста на 24 км/ч больше,чем скорость всадника, если скорость всадника 16 км/ч, то скорость мотоциклиста: 
                                                24+16=40 км/ч;
Найдя скорость мотоциклиста, найдем, сколько времени он потратил на этот путь. Для этого используем формулу нахождение времени:
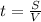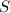t= \frac{S}{V} , где S - длина пройденного расстояние,а 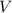V- скорость мотоциклиста.
                                                     S= 80 км;
                                                     V= 40 км/ч;
                                    Подставляем данные у формулу:
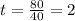t= \frac{80}{40}=2 часа - время. которое было потрачено мотоциклистом, что бы пройти расстояние 80 км.
                                                    ответ:
                       2 часа потратил на этот путь мотоциклист 
  
4,4(70 оценок)
Это интересно:
О
Как составить план: секреты планирования на будущее...
И
Школа дома: как не потеряться и организоваться...
Д
Дом-и-сад
03.02.2020
Как быстро и эффективно избавиться от шоколадных пятен...
Х
Как сделать светящуюся палочку: пошаговая инструкция...
П
Как выращивать кроликов ради мяса или шерсти...
З
Здоровье
22.01.2023
Как сделать мешочек с кукурузой: всё, что нужно знать...
К
Как словить покемона Кресселию...
02.01.2020
Как стать серьезным: 10 советов от успешных людей...
С
Как справиться с ребенком, который постоянно говорит нет...
К
Как легко и быстро распечатывать с Samsung Galaxy Note 3...
Новые ответы от MOGZ: Другие предметы
melnikmaryana
melnikmaryana
02.01.2022
1. найдите в конституции рф и составьте письменно перечень вопросов , по которым приняты и действуют фкз 2. найдите решение конституционного суда рф, которое. по вашему...
Sofia20091
Sofia20091
28.03.2023
Заранее ! 30 ! rewrite the sentences using the structure ‘have something done’. 1) i made the necklace. 2) i delivered the furniture. 3) i wrote the report. 4) i repaired...
sofa287
sofa287
11.03.2022
Написать сочинение c3 по этому тексту...
hrustam2004
hrustam2004
28.03.2023
Координаты крайних точек южной америки мыс гальинас мыс париньяз мыс кабу-бранку мыс горн мыс фроуард зарание...
filatevanastya1
filatevanastya1
27.07.2022
Напишите маленький конспект по теме сказка зарание : з...
jfksbsj
jfksbsj
08.06.2022
Площа діагонального перерізу прямокутного паралелепіпеда дорівнює 60 кв.см., а діагональ основи - 12 см. знайдіть довжину діагоналі паралепіпеда. ​...
tach11
tach11
28.03.2023
Втреугольник abc ,сторона ab=10 дм ,высота bd ,проведенная к стороне ac равна 8 дм ,dc=15 дм. найдите площадь треугольника...
Ученик705
Ученик705
17.07.2022
Вычислите массовые доли элементов в гидрооксиде натрия...
Erikalallala
Erikalallala
28.03.2023
Напишите сочинение на тему незабываемый день сочинение надо большое...
lunnui
lunnui
04.04.2023
Слухи - лучшие пресс агенты. брюс бартон (1886-1967), американский рекламный агент. необходимо расписать свое мнение, касательно этого афоризма. значение, смысл, личное...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ