ответ: Из известных сегодня спутников, такого спутника нет.
Объяснение: Дано:
Диаметр Солнца D = 1,392*10^6 км
Диаметр Сатурна d = 116464 км
Расстояние от Солнца до Сатурна R = 1429394069 км
Найти расстояние от спутника Сатурна до планеты r - ?
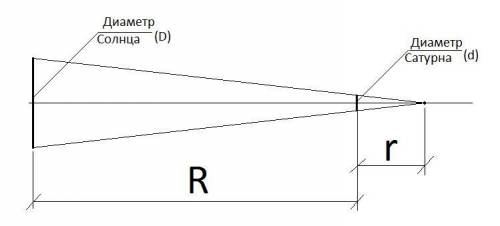
Чтобы определить, какой спутник изображен на рисунке художника, надо найти расстояние (r) с которого наблюдаемый угловые диаметры Солнца и Сатурна будут одинаковыми (см. рисунок). Из подобия треугольников можно составить соотношение: D/(R + r) = d/r. Из этого уравнения r = d*R/(D – d) = 116464*1429394069/(1392000 – 116464) = 130512153,99 км.
Из известных сегодня спутников Сатурна ни один спутник не находится так далеко от планеты. Самый дальний из известных спутников находится на расстоянии 25108000 км. . Это расстояние в 5,198 раз меньше найденного расстояния r. Следовательно, с самого дальнего из известных спутников Сатурна угловой диаметр Сатурна будет в 5 с лишнем раз больше углового диаметра Солнца. Таким образом, при написании картины художник ошибся в относительных угловых размерах Солнца и Сатурна.
Однажды Будда пришёл на встречу со своими учениками с носовым платком, с очень ценным носовым платком. Возможно, какой-то царь подарил его. Но Будда не приемлет таких вещей, поэтому все смотрели и думали: «В чём дело? Почему он несёт его в руке, держа перед собой, как бы говоря каждому: "Смотрите, внимательно смотрите!" Смотреть было не на что. Это был всего лишь красивый шёлковый носовой платок. Затем Будда начал завязывать узлы на нём, пять узлов. Стояло полное молчание..., все смотрели на то, что он делает. Будда с учеников:
— Это тот же самый носовой платок, который я принёс с собой, или это другой носовой платок?
Шарипутра, один из его старших учеников, встал и сказал:
— Вы шутите с нами? Я думаю, что это тот же самый носовой платок.
Будда сказал:
— Шарипутра, подумай ещё раз: так как у носового платка, который я принёс, не было узлов, а у этого их пять. Как же он может быть тем же самым?
Шарипутра увидел смысл и сказал:
— Я всё понял. Хотя это тот же носовой платок, но теперь он в узлах подобно страдающему человеку.
— Совершенно точно. Вот что я хочу показать вам: человек, который терзается, не отличается от Гаутамы Будды. Я лишь носовой платок без узлов. Ты — носовой платок с пятью узлами (пять узлов — агрессивность, алчность, лживость, неосознанность и эгоизм).
Затем Будда сказал:
— Я хотел бы с вас ещё об одной вещи. Я пытаюсь развязать эти узлы. Взгляните на меня: это развязать их?
Он потянул за оба конца носового платка, узлы сделались ещё меньше и туже. Кто-то сказал:
— Что Вы делаете? Таким узлы никогда не развяжутся. Такой тонкий шёлк, а вы так сильно тянете! Узлы становятся маленькими, и их теперь почти невозможно развязать!
Будда сказал:
— Вы можете так ясно понять всё относительно этого носового платка. Разве вы не можете понять самих себя? Разве вы не видите себя в такой же ситуации? Вы тянули свои узлы или нет? Иначе почему они продолжают становиться всё меньше и меньше, туже и туже?
Затем Будда с Что же я должен сделать?
Один монах встал и предложил:
— Сначала я хотел бы подойти поближе и посмотреть, как были завязаны узлы. Он взглянул на носовой платок и сказал:
— Узлы были сделаны таким образом, что, если мы расслабим их и позволим им стать более свободными, они развяжутся — это нетрудно. Это узлы. Будда дал монаху носовой платок и тот развязал узлы один за другим.
Будда сказал:
— Сегодняшняя проповедь закончена. Идите медитируйте!
Объяснение:
15: 3 =5(.см)
вторая сторона 5 см
Периметр равен сумме всех сторон прямоугольника
Р= 5+5+3+3= 16 см