Испаряясь с поверхности водоемов, почвы, растений, вода накапливается в атмосфере и, рано или поздно, выпадает в виде осадков, пополняя запасы в океанах, реках, озерах и т.п. Таким образом, количество воды на Земле не изменяется, она только меняет свои формы - это и есть круговорот воды в природе.
Круговорот кислорода в биосфере весьма сложен, поскольку он вступает во множество химических соединений минерального и органического миров. Свободный кислород современной земной атмосферы является побочным продуктом процесса фотосинтеза зеленых растений и его общее количество отражает баланс между продуцированием кислорода и процессами окисления и гниения различных веществ.
С азотом фосфором и т.д. Так же
Испаряясь с поверхности водоемов, почвы, растений, вода накапливается в атмосфере и, рано или поздно, выпадает в виде осадков, пополняя запасы в океанах, реках, озерах и т.п. Таким образом, количество воды на Земле не изменяется, она только меняет свои формы - это и есть круговорот воды в природе.
Круговорот кислорода в биосфере весьма сложен, поскольку он вступает во множество химических соединений минерального и органического миров. Свободный кислород современной земной атмосферы является побочным продуктом процесса фотосинтеза зеленых растений и его общее количество отражает баланс между продуцированием кислорода и процессами окисления и гниения различных веществ.
С азотом фосфором и т.д. Так же
1)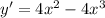
Произведение ранво нулю, когда один из множителей равен нулю.
4x = 0
Имеем три точки экстремума.
2)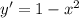
Мы нашли точку экстремума равной -1, которая находится на нашем промежутке. Теперь надо понять, является она максимумом или минимумом. Для этого берем любое значение из промежутка до -1. Например, x = -2, и подставляем в производную.
y'(-2) < 0
Значит на этом промежутке функция убывает, т.е x = -1 это точка минимума.А значит в этой точке функция имеет наименьшее значение на данном промежутке.
Подставляем x = -1 в функцию.
ответ: у = -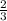
3)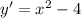
Мы нашли точку экстремума равной 2, которая находится на нашем промежутке. Теперь надо понять, является она максимумом или минимумом. Для этого берем любое значение из промежутка до 2. Например, x = 0, и подставляем в производную.
y'(0) < 0
Значит на этом промежутке функция убывает, т.е x = 2 это точка минимума.А значит в этой точке функция имеет наименьшее значение на данном промежутке. А нам нужно наибольшее значение. Поэтому находим значения функции на границах данного промежутка. Т.е в x = 0 и x = 3.
y(0) =.0
y(3) = 9 - 12 = -3
Получаем, что y(0) > y(3), значит в точке x = 0 функция имеет наибольшее значение на данном промежутке.
ответ: у = 0