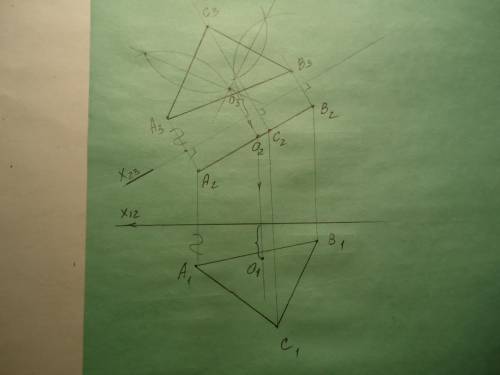
Построение проекций точки, равноудалённой от вершин треугольника АВС, см. на фото.
Объяснение:
Применим метод замены плоскостей проекций:
Проведём плоскость параллельно проекции А₂В₂С₂ и построим натуральную величину треугольника АВС - А₃В₃С₃. Расстояние от оси х₁₂ до точек А₁, В₁ и С₁ равно расстоянию от новой оси х ₂₃ до точек А₃, В₃ и С₃.
Точкой, равноудалённой от вершин треугольника является центр описанной окружности, который находится на пересечении серединных перпендикуляров к сторонам треугольника.
Строим хотя бы два серединных перпендикуляра к сторонам треугольника А₃В₃С₃ с циркуля. Их точку пересечения обозначим О₃.
Находим проекцию О₂ на проекции А₂В₂С₂ и переносим её на проекцию треугольника А₁В₁С₁ с расстояния, отмеченного фигурной скобкой, получим О₁.
(Извините, что сначала дала ответ на прежний ваш вопрос, невнимательно прочитав задание.)
Надеюсь, что смогла вам Удачи
α=30градусов вроде
2*(корень из 2/2)все это в квадрате+2*соs(3*30гадусов)все тоже в квадрате+sin(6*30)
откроем скобки:2*2/4+2*0+0=4/4=1
1=1