Бег на короткую дистанцию в один стадий (192,27 м), С 724 г.до н.э. добавили бег на дистанцию в 2 стадия (384,54 м).
В 720 г.до н.э. была введена длинная дистанция - круг длиной в стадий (стадион) надо было пробежать 24 раза (4614 м).
С 708 г.до н.э. - пятиборье (пентатлон): прыжки, бег, метание диска, метание копья (дротика), борьба;
С 688 г.до н.э. - кулачный бой;
С680 г.до н.э. - состязания на колесницах, запряженных четверкой лошадей; в середине VII в.до н.э. добавился панкратий - борьба, в которой были разрешены любые приемы.
В 632 г.до н.э. допустили молодежь на соревнования по бегу, борьбе, кулачному бою. Впоследствии - гонки воинов в полном вооружении на колесницах с парой лошадей, скачки на жеребятах.
Объяснение:
всё
Объяснение:
Вариант 1:
1. (xVy)↔(y↓⌐x),
(x│⌐y)→(z+⌐(xy));
2. x→(y+z),
(x→y)+(x→z);
3. (xV⌐y)→(⌐z+⌐x);
4. f(0,1,0)=f(1,0,0)=f(1,0,1)=0;
5. f=(1101 1101 0011 0011);
6. J={xVy, ⌐x+y}.
Вариант 2:
1. (x↔⌐y)V(y↓x),
((x→⌐y)│⌐z)+⌐(xy);
2. x│(y→z),
(x│y)→(x│z);
3. ⌐((xV⌐y)→(z+⌐x));
4. f(0,1,1)=f(1,0,0)=f(1,1,0)=0;
5. f=(1111 1100 1011 1011);
6. J={x→y, ⌐x⌐y}.
Вариант 3:
1. (xV⌐y)↔(y↓x),
((x│⌐y)→z)+⌐(xy);
2. x(y+z),
xy+xz;
3. (⌐xV⌐y)→ ⌐(z+x);
4. f(0,0,0)=f(0,0,1)=f(1,0,1)=f(1,1,1)=1;
5. f=(1110 0101 0011 0101);
6. J={x↔y, ⌐x│⌐y}.
Вариант 4:
1. (x↔⌐y)V(y↓x),
((x→⌐y)│⌐z)+⌐(xy);
2. x(y+z),
xy+xz;
3. (xV⌐y)→ ⌐(z↔⌐x);
4. f(0,0,1)=f(1,1,1)=f(1,1,0)=0;
5. f=(1101 0011 1101 0011);
6. J={x+y, ⌐xVy}.
Вариант 5:
1. (xV⌐y)→(y+x),
((x↔⌐y)│⌐z)↓⌐(xy);
2. x(y→z),
xy→xz;
3. ⌐((xV⌐y)→(z↔⌐x));
4. f(0,0,0)=f(1,1,1)=f(1,1,0)=0;
5. f=(1100 1011 1111 1011);
6. J={⌐x→y, x⌐y}.
Вариант 6:
1. (x+⌐y)↔(y│x),
((x↓y)↔⌐z)V⌐(xy);
2. x(y↔z),
xy↔xz;
3. ⌐((x│⌐y)+(z→⌐x));
4. f(0,0,1)=f(0,1,1)=f(1,1,0)=f(1,1,1)=1;
5. f=(0101 0101 1110 0011);
6. J={⌐x↔y, x│⌐y}.
Вариант 7:
1. (xV⌐y)↓(y→x),
((x│⌐y)↔⌐z)+⌐(xy);
2. x(y│z),
xy│xz;
3. ⌐((z→x)↔(y│x));
4. f(0,0,0)=f(1,0,1)=f(1,1,1)=0;
5. f=(0011 0011 1101 1101);
6. J={x+⌐y, ⌐xVy}.
Вариант 8:
1. (x+⌐y)→(y↓x),
((x│⌐y)V⌐z)↔⌐(xy);
2. xV(y→z),
(xVy)→(xVz);
3. (x│⌐y)+(⌐z→x);
4. f(1,0,1)=f(0,1,0)=f(1,1,1)=0;
5. f=(1011 1011 1100 1111);
6. J={x→⌐y, ⌐xy}.
Вариант 9:
1. ⌐x↔(y→(⌐y↓x)),
((⌐x│y)V⌐z)+⌐(xy);
2. xV(y│z),
(xVy)│(xVz);
3. (⌐z→x)↔(⌐x│y);
4. f(1,0,0)=f(1,1,0)=f(0,1,1)=f(0,1,0)=1;
5. f=(0101 0011 0101 1110);
6. J={x↔⌐y, ⌐x│y}.
Вариант 10:
1. x↓(⌐y→(y↓x)),
x+(⌐yV⌐z↔⌐(xy));
2. xV(y↔z),
(xVy)↔(xVz);
3. (z→x)+(x│⌐y);
4. f(0,1,1)=f(1,0,0)=f(1,0,1)=0;
5. f=(0011 1101 0011 1100);
6. J={⌐x+⌐y, xV⌐y}.
Вариант 11:
1. x↔(⌐y→(y+x)),
x│(⌐yV⌐z↓⌐(xy));
2. x+(y↔z),
(x+y)↔(x+z);
3. ((x↓y)→z)+y;
4. f(0,0,1)=f(1,0,0)=f(1,1,0)=0;
5. f=(1011 1111 1011 1100);
6. J={xy, ⌐x→⌐y}.
Вариант 12:
1. x→(⌐y│(y+x)),
x↔(⌐yV⌐z↓⌐(xy));
2. x+(y→z),
(x+y)→(x+z);
3. ⌐((x│y)→z)+y;
4. f(0,0,1)=f(0,1,1)=f(1,1,1)=0;
5. f=(0011 1110 0101 0101);
6. J={x│y, ⌐x↔⌐y}.
Вариант 13:
1. x↓(⌐y→(yVx)),
x│(⌐y↔⌐z+⌐(xy));
2. x+(y│z),
(x+y)│(x+z);
3. ⌐((x↓y)→⌐z)+y);
4. f(0,0,0)=f(0,0,1)=f(1,1,0)=0;
5. f=(0011 0011 1100 1111);
6. J={⌐x+y, ⌐xV⌐y}.
Вариант 14:
1. x+(⌐y→(y↔x)),
x↓(⌐yV⌐z│⌐(xy));
2. x↓(y↔z),
(x↓y)↔(x↓z);
3. (⌐(x↓y)→⌐z)↔y;
4. f(0,0,0)=f(0,1,0)=f(1,1,1)=0;
5. f=(1100 0101 0011 0011);
6. J={xy, x→⌐y}.
Вариант 15:
1. (x↓y)│(yV⌐x),
(x↔⌐y)+(z→⌐(xy));
2. x│(y+z),
(x│y)+(x│z);
3. ⌐(((x↓y)→⌐z)↔y);
4. f(0,0,0)=f(0,0,1)=f(1,0,0)=f(1,1,0)=1;
5. f=(0010 0111 1010 1101);
6. J={xVy, ⌐x↔y}.
Вариант 16:
1. (x│y)→(y+⌐x),
(x⌐y)V(z↔⌐(x↓y));
2. x→(y│z),
(x→y)│(x→z);
3. (⌐(x↓y)→⌐z)+y;
4. f(1,0,1)=f(0,1,1)=f(0,1,0)=0;
5. f=(0011 1111 0011 1100);
6. J={x+y, xV⌐y}.
Вариант 17:
1. (xVy)→(y↓⌐x),
(x│⌐y)↔(z+⌐(xy));
2. x→(y↔z),
(x→y)↔(x→z);
3. ⌐((xVy)→(⌐z↔y));
4. f(1,0,0)=f(0,1,1)=f(0,1,0)=0;
5. f=(0101 0011 1100 0011);
6. J={x⌐y, ⌐x→⌐y}.
Вариант 18:
1. (xVy)↓(y→⌐x),
(x+⌐y)→(z│⌐(xy));
2. xV(y+z),
(xVy)+(xVz);
3. ⌐((x│y)+(⌐z→y));
4. f(0,0,1)=f(0,1,1)=f(1,0,0)=f(1,0,1)=1;
5. f=(0111 1101 0010 1010);
6. J={x↓⌐y, ⌐x↔⌐y}.
Вариант 19:
1. (x+y)│(y↓⌐x),
(x↔⌐y)→(zV⌐(xy));
2. x↓(y+z),
(x↓y)+(x↓z);
3. ⌐(((x↓y)→z)↔x);
4. f(1,0,0)=f(0,0,1)=f(0,1,1)=0;
5. f=(1111 1100 0011 0011);
6. J={x+⌐y, xVy}.
Вариант 20:
1. xy↔(y↓⌐x),
(x→⌐y)│(z+⌐(xVy));
2. x↔(y+z),
(x↔y)+(x↔z);
3. (⌐xVy)→⌐(⌐z↔y);
4. f(0,0,1)=f(0,1,1)=f(1,1,0)=0;
5. f=(0011 0011 0101 1100);
6. J={x→y, ⌐xy}.
Вариант 21:
1. x↓(⌐y+(y→⌐x)),
xV(⌐y│⌐z+⌐(xy));
2. x→(y↓z),
(x→y)↓(x→z);
3. ⌐(((x↔y)│⌐z)+y);
4. f(0,0,0)=f(0,0,1)=f(1,0,0)=f(1,1,0)=0;
5. f=(1110 1001 0111 0001);
6. J={⌐x↓y, ⌐x↔⌐y}.
Вариант 22:
1. x│(⌐y+(yVx)),
x→(⌐y↓(⌐z↔⌐(xy)));
2. x↓(y│z),
(x↓y)│(x↓z);
3. ⌐(x↓y)→(z↔⌐y);
4. f(0,1,1)=f(1,0,0)=f(1,0,1)=1;
5. f=(0001 0011 1100 1110);
6. J={⌐x+⌐y, ⌐xVy}.
Вариант 23:
1. x+(⌐y→(y↔⌐x)),
x↓(⌐y│(zV⌐(xy)));
2. x↔(y│z),
(x↔y)│(x↔z);
3. ⌐(((x↓y)→⌐z)↔y);
4. f(0,0,1)=f(1,0,0)=f(1,1,0)=1;
5. f=(0011 1100 0011 0101);
6. J={⌐x⌐y, ⌐x→y}.
Вариант 24:
1. x↔(y(⌐y→x)), xV(⌐y+(z↓⌐(x│y)));
2. x→(y↓z),
(x→y)↓(x→z);
3. (⌐(x↔y)→⌐z)│y;
4. f(0,1,1)=f(0,1,0)=f(1,0,1)=f(1,1,1)=1;
5. f=(0011 1101 0010 1100);
6. J={xV⌐y, ⌐x↔y}.
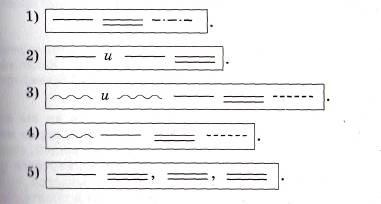
2 Итак, у вас уже есть какая-то начальная схема предложения. Если вы уберёте сами слова и оставите только линии, которыми подчёркиваются члены предложения, то это уже можно считать схемой. Однако, предположим, в вашем случае всё сложнее. У вас, например, предложение осложнённое, то есть, например, в нём есть деепричастный оборот. Такой оборот полностью подчёркивается как обстоятельство, а на схеме будет отделяться от остальных линий вертикальными чёрточками: ,|_._._._._|,
3 Если у вас сложное предложение, то на схеме нужно будет отразить все предикативные части, которые вы найдёте в этой громаде. Предикативную часть можно выделить посредством поиска в предложении всех грамматических основ: одна грамматическая основа - одна предикативная часть. То есть, если у нас сложносочинённое предложение (то есть, части в нём равноправны и одна от другой никак не зависит) , то обе части мы будем выделять квадратными скобками, а между ними поместим знак препинания и союз, который их соединяет: [], и [].
4 Если же у вас сложное предложение, то вам придётся показать все взаимосвязи между частями, поскольку в таком предложении одна часть подчиняется другой. Та, которой подчиняются, - главная, та, которая подчиняется, - придаточная. Главная обозначается квадратными скобками, придаточное - круглыми: [], (который.. . ). Такая схема будет уместна для предложения, например: "Мы увидели дом, который построил Джек", и предложение будет сложноподчинённым с придаточным определительным.
5 При составлении схемы учитывайте требования вашего преподавателя, поскольку требования эти могут различаться. Также не забывайте, что схема - это как бы прелюдия к разбору предложения, поэтому чем больше вы напишете в схеме, тем больше сможете понять и потом сказать. Но не перегружайте схему: например, зачастую ни к чему показывать на схеме большого сложноподчинённого предложения все члены предложения, которые там есть. Можно отметить только грамматическую основу.