Запишем 2 закон Ньютона для проекций на вертикальную ось направленную вверх: m *a = F - m *g, где m - масса тела, a - ускорение движения, F - сила, с которой пол ракеты действует на груз, m *g - сила тяжести.
Силу F выразим по формуле: F = m *a + m *g = m *(a + g) = m *(3 *g + g) = 4 *m *g.
Согласно 3 закона Ньютона, сила F, с которой пол давит на груз, равна силе Р, с которой груз на пол, то есть весу груза.
Р = 4 *m *g.
Р = 4 *10 кг *9,8 м/с^2 = 392 Н.
ответ: вес груза при движении ракеты Р = 392 Н.
Радиус окружности: R = 20 м.
Пройденный путь: S = L/4.
Найти путь S - ? и модуль перемещения r - ?
А также определить отношение скоростей: <Vп>/<Vr> - ?
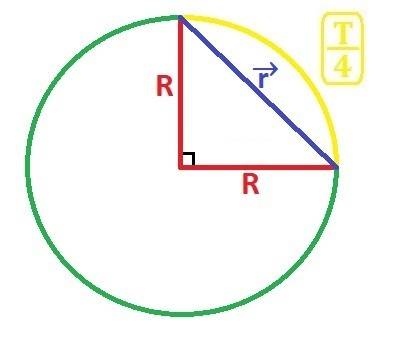
Решение:0. Немного фирменных рисунков, смотри приложение.
1. Чтобы найти путь для начала найдём длину окружности. Формула длины окружности: L = 2πR.
2. Путь, пройденный телом - четверть длины окружности: 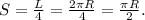
3. Перемещение найдём по теореме Пифагора (см. приложение): 
4. Средняя путевая скорость: 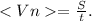
5. Средняя скорость по перемещению: 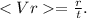
6. Искомое отношение: 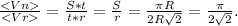
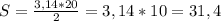 (м).
(м).
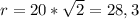 (м).
(м).
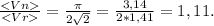
73 рад/с
Объяснение:
Дано:
L = 30 см = 0,30 м
r = L/2 - это расстояние от края стержня до середины.
V = 10 м/с
m = M
ω - ?
1)
Момент инерции однородного тонкого стержня массой М и длиной L, если ось вращения проходит через центр тяжести стержня:
J₁ = M·L² /12
Момент инерции пули m относительно центра тяжести:
J₂ = m·r²/2 = m·(L/2)² / 2 = m·L²/8
Суммарный момент инерции:
J = J₁+J₂ = M·L² /12 + m·L²/8
Учтем, что m = M, тогда:
J = J₁+J₂ = m·L² /12 + m·L²/8 = 5·m·L² / 24 = 5·0,3²·m/24 ≈ 0,0188·m
2)
Кинетическая энергия стержня:
T = (1/2)·J· ω² = 0,0188·m·ω²/2 =0,0094·m·ω²
Кинетическая энергия пули:
T₁ = m·V²/2 = m·10²/2 = 50·m
3)
По закону сохранения энергии:
T = T₁
0,0094·m·ω² = 50·m
0,0094·ω² = 50
ω = √ (50/0,0094) = √ 5320 ≈ 73 рад/с