1)U=IR = 20 Ом × 0,4 А=8 В
2)R=ρl/s , s=ρl/R=(0,5 Ом × мм²/м × 8м) /2 Ом= 2мм²
3)правильное условие
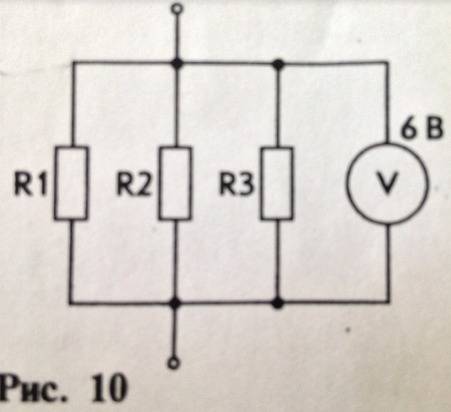
Определите общее сопротивление цепи и силу тока в неразветвленной части цепи ,если R1=30 Ом, R2=10 Ом, R3= 30 Ом, V=6В.
схема рис 10 Решение во вкладке.
4)R=ρl/s , ρ=Rs/l=Us/ (IL)=0,4 Ом × мм²/м² R=U/I (по закону Ома) ответ:ρ=0,4 Ом × мм²/м²(никелин)
5. Определите общее сопротивление цепи и напряжение на концах участка АВ, если R1=4 Ом, R2 =6 Ом, R3 = 15 Ом, R4 = 4 ом
схема на рис 1 решение в скане
6. Определите общее сопротивление цепи если R1 = 4 Ом, R2 = 6 Ом,
R3 = 12 Ом, R4 = 12 Ом, R5 = 6 Ом
схема на рис 2 решение в скане
7. По этой задаче не нашел данных.
F = γmM/(h+R)², вызывающая ускорение свободного падения
a = γM/(h+R)²
M - масса Земли
γ - гравитационная постоянная
R - радиус Земли - 6 400 000 м
Чтобы не путаться в порядках большой величины M и малой величины γ предпочитаю где возможно использовать равенство
γM = gR²
g - ускорение свободного падения близ поверхности Земли
Условием движения по круговой орбите радиуса (h + R) c орбитальной скоростью v является равенства упомянутого ускорения
a = gR²/(h+R)²
центростремительному ускорению
a = v²/(h+R)
Из уравнения
gR²/(h+R)² = a = v²/(h+R)
можно получить значение для орбитальной скорости:
v² = gR²/(h+R)
Для случая h = R это выражение принимает вид:
v² = gR²/2R = gR/2
v = √(gR/2) = √(10*6400000/2) = √32000000 = 5660 м в сек (5,66 км в сек)