t = 11,7 сек. (приближенно)
Объяснение:
Учитывая, что начальная скорость вертолете ноль, найдем высоту h, на которую он поднялся за время t по формуле
h = a
/2 (1), здесь a - ускорение с которым поднимается вертолет.
Подставляя данные из условия в формулу (1) получим. h = 4*
/2 = 200 метров. Скорость V с которой движется вертолет составит V = at = 4*10 = 40 м/сек.
Теперь для предмета, упавшего из вертолета: его начальная скорость будет равна скорости вертолета, т.е. 40 м/сек и вектор скорости направлен вверх. На предмет будет действовать сила тяжести, придающая ему ускорение g = 9,8 м/сек, направленная вниз. Таким образом, за время t = V/g (2) скорость предмета станет равной нулю. Подставляя в (2) наши данные получим, t = 40/9,8 = 4,08 сек. За это время предмет дополнительно поднимется на высоту
h1 = Vt - g/2 = 40*4,08 - 10*16,64/2 = 81,63 м.
h2 = h+h1 = 200 + 81,63 = 281,63
Для тела, падающего с высоты h2 без начальной скорости имеем
h2 = g/2
Отсюда получаем t = 
= 
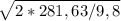= 7,58 сек
К этому времени надо добавить 4,08 сек, что предмет летел вверх. Получаем
t = 7,58 + 4,08 = 11,66 сек. = 11,7 сек.
Исходные данные:
Скорость потока жидкости W = 2,0 м/с;
диаметр трубы d = 100 мм;
общий напор Н = 8 м;
относительная шероховатость 4·10-5.
Решение задачи:
Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.
Значение скоростного напора определяется по соотношению:
w2/(2·g) = 2,02/(2·9,81) = 0,204 м
Потери напора воды на местные сопротивления составят:
∑ζМС·[w2/(2·g)] = (4,1+1)·0,204 = 1,04 м
Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):
hп = H - (p2-p1)/(ρ·g) - = 8 - ((1-1)·105)/(1000·9,81) - 0 = 8 м
Полученное значение потери напора носителя на трение составят:
8-1,04 = 6,96 м
Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10-3 Па·с, плотность воды – 1000 кг/м3):
Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10-3) = 200000
Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):
λ = 0,316/Re0,25 = 0,316/2000000,25 = 0,015
Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:
l = (Hоб·d) / (λ·[w2/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м
ответ:требуемая длина трубопровода составит 213,235 м.