Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.
Действующее значение переменного тока - это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Объяснение:
ну как то так
Дано:
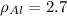 г/см³;
г/см³;
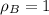 г/см³;
г/см³;
 Н;
Н;
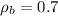 г/см³;
г/см³;
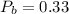 Н;
Н;
____________
Найти: 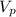
СИ: 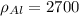 кг/м³;
кг/м³; 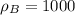 кг/м³;
кг/м³; 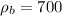 кг/м³;
кг/м³;
Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):
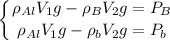
Или, подставив численные значения величин:
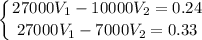
Вычитая из первого второе уравнение, найдем внешний объем шарика:
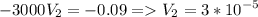 м³
м³
Подставляя результат в первое уравнение, найдем объем метала в шарике:
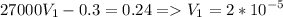 м³
м³
Объем полости:
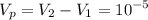 м³ или 10 см³
м³ или 10 см³
ответ: 10 см³.
Путь 89/4 модуль = L89/4*корень2