Задача решается методом эквивалентного сопротивления (метод основан на замене нескольких сопротивлений в цепи одним эквивалентным, не влияющим на токораспределение в остальной части цепи).
Наблюдается последовательное соединение двух групп параллельно соединенных резисторов (соединенные параллельно R1, R2 и R3 последовательно соединенным с соединенными параллельно R4 и R5)
Эквивалентное сопротивление для первой группы составит
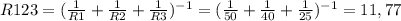 Ом.
Ом.
Эквивалентное сопротивление для второй группы составит
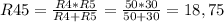 Ом.
Ом.
Эквивалентное сопротивление цепи
Rэ = R123+R45 = 11,77+18,75 = 30,52 Ом.
Тогда – по закону Ома – ток в неразветвленной части цепи
I = U/Rэ = 250/30,52 = 8,19 А.
Падение напряжения на второй группе (по тому же закону Ома)
U45 = I*R45 = 8,19*18,75 = 153,61 В.
Падение напряжения на первой группе
U123 = I*R123 = 96,39 В.
Тогда токи через резисторы
I1 = U123/R1 = 96,39/50 = 1,93 А;
I2 = U123/R2 = 96,39/40 = 2,41 А;
I3 = U123/R3 = 96,39/50 = 3,86 А;
I4 = U45/R4 = 153,61/50 = 3,07 А;
I5 = U45/R5 = 153,61/30 = 5,12 А.
2 Ома
Объяснение:
p=40*10^–8 Ом × м
L= 4 м
d= 1 мм. = 0.001 м
S=п*(d/2)^2
R=p*L/S = p*L*4 / (п*d^2) = 40*10^–8 *4*4 / (3.14*0,001^2) = =2 Ома