ответ: Высота полета спутника над Землей ≈ 9545 км
Объяснение: Похоже, что в условии задачи имеется ошибка. Дело в том, что орбитальная скорость Луны, которая находится от Земли на расстоянии 384000 км, немного превышает 1 км/с. Если принять, что скорость некоторого спутника = 5м/с, то тогда он должен находится от Земли на расстоянии более 15 миллионов км. Но, тогда этот спутник перестанет быть спутником Земли, а станет спутником Солнца. Так что, думаю, что в условии задачи скорость спутника = 5 км/с.
Квадрат линейной (орбитальной) скорости спутника Земли определяется выражением V² = G*Mз/(Rз + h). Здесь G - гравитационная постоянная; Mз - масса Земли = 5,9726*10^24 кг; Rз - радиус Земли = 6400000 м; h - высота полета спутника. Из этой формулы h = (G*Mз/V²) - Rз = (6,67430*10^-11 * 5,9726*10^24/5000²) - 6400000 ≈ 9545169,7 м ≈ 9545 км
1. Существует формула ν=n/t, где ν - частота, n - кол-во колебаний, а t - время колебаний. Переведём 9.5 мин в секунды и получим 570 сек. Подставим в формулу: ν=40/570≈0.07 Гц. ответ: 0.07 Гц
2. Для решения данной задачи нам потребуется формула T=2π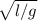
, где T - период колебаний, π - число пи, ≈ равное 3,14, ℓ - длинна маятника, равная 0.35м=35см и g - ускорение свободного падения, равное 9,8 м/с(Н/кг).
T=2π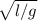
T=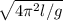
T≈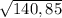
T≈11,86
ответ: 11,86 сек
3. Период колебаний(Т) равен 1 сек;
частота колебаний(ν) равна 1 Гц (по формуле ν=1/Т и др.);
амплитуда колебаний(А) равна 0.05 м=5 см.
ответ: 1 сек; 1 Гц; 5см