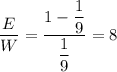Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда ⇒ (1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть , но согласно уравнению (1) получим
Аналогично , однако мы знаем, что
Тогда ⇒ , а это значит что
Поэтому , так как , то ⇒ (2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1) ⇒ , следовательно
№ 1 выигрыш в силе n = 80 см / 20 см = 4 раза № 2 ΔL = 10 м За 1 оборот L = 2*π*R => N = ΔL / L = ΔL / (2*π*R) = 10 м / (2*3,14*0,20 м) ≈ 8 № 3 Ведро наполнено на 3/4 сл-но 12 л * 3/4 = 9 л воды в ведре, это 9 кг воды + масса ведра 1 кг итого ведро с водой имеет массу 10 кг Работа силы тяжести по модулю A = mgh = 10 кг * 9,81 м/с² * 9 м ≈ 883 Дж ≈ 0,88 кДж №4 ΔП = Δm*g*Δh Δm = ρ*V = ρ*π*d²*Δl/4, Δl = 0,4 м, d = 1,13 м, Δh = H + Δl/2 Δh = 10,2 м высота подъема воды из колодца ΔП = 1000 кг/м³ * 3,14 * (1,13 м)² * 0,4 м * 9,81 м/с² * 10,2 м / 4 ≈ 40120 Дж ≈40 кДж - увеличилась
ответ: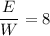
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда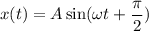 ⇒
⇒ 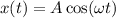 (1)
(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть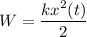 , но согласно уравнению (1) получим
, но согласно уравнению (1) получим 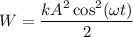
Аналогично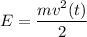 , однако мы знаем, что
, однако мы знаем, что 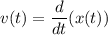
Тогда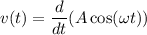 ⇒
⇒ 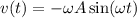 , а это значит что
, а это значит что 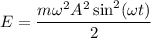
Поэтому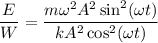 , так как
, так как 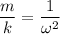 , то
, то 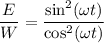 ⇒
⇒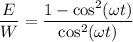 (2)
(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)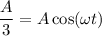 ⇒
⇒ 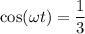 , следовательно
, следовательно 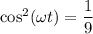
Возвращаясь к уравнению (2) получим