Выберем направление для ускорения - вверх для висящего тела и соответственно вниз по накл. плоскости для другого тела.
Тогда для висящего на блоке тела:
T - m1g = m1a (1)
Для тела, скользящего по наклонной плоскости, в проекциях на оси Х и У:
(ось Х - по направлению предполагаемого движения, осьУ - нормаль к пов-ти накл. пл-ти)
Х: m2g*sina - kN - T = m2a
Y: N - m2g*cosa = 0, где k - коэфф. трения, N - сила реакции опоры.
Подставив из второго значение для N в первое, получим:
T = m2g(sina - kcosa) - m2a (2)
Вычтем из (2) (1):
m1g = m2g(sina - kcosa) - (m1+m2)a
Отсюда находим ускорение :
a = (g*(m2(sina-kcosa)-m1)) / (m1+m2)
Подстановка числовых значений приводит к отрицательному значению.
Поменяв направление движения на противоположное, получим выражение для ускорения:
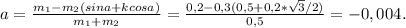
Делаем вывод, что сила трения покоя не позволяет данной системе тел начать движение. Система покоится. а = 0.
Тогда натяжение нити просто равно:
T = m1g = 2 Н
ответ: а = 0; Т = 2 Н.
Voх=10м/с- проекция начальной скорости тела на ось Ох
Хо=0 абсцисса начального положенияния тела
х- абсцисса кончного положения тела, в момент падения его на землю
Voy=0- проекция начальной скорости тела на ось Оу
Уо=L- ордината начального положения тела,в момент падения его на землю
По условию х=L
Так как тело по оси Ох движется равномерно, то х=Vox*t. Отсюда t=x/Vox=L/Vox
Тело по оси Ох движется равноускоренно по закону
у=уо+Voy*t-gt2(квадрат)/2 или 0=L-g*t2(квадрат)/2.
Отсюда vox*t=g*t2/2, t=(2*Vox/g=2c
L=h=10*2/9,8=20м