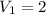м3 - объем льдины над водой 
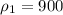кг/м3 - плотность льда 
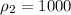кг/м3 - плотность воды Найти массу 
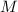льдины Решение. На плавающую равномерно и прямолинейно льдину действуют сила Архимеда 
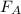сила тяжести 
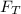. Из первого закона Ньютона имеем: 
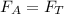--------(1) При этом 
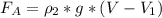------(2) где 
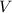- объем льдины В свою очередь 
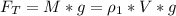------(3) где 
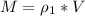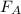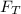--------(4) Подставим в (1) вместо и выражения (2) и (3): 
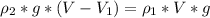, сокращая на 
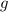, выразим : 
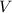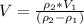-------(5) И, наконец, подставим в (4) вместо 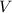выражение (5), найдем : 
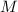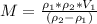----(6) Расчет массы льдины по формуле (6): 
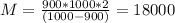кг
Будем считать, что сила трения качения пренебрежимо мала, а также пренебрежем сопротивлением воздуха. Тогда для обоих случаев должен выполняться закон сохранения полной механической энергии.
1) Таким образом в обоих случаях цилиндры движутся под действием составляющей силы тяжести параллельной наклонной плоскости. Из второго закона Ньютона получим:
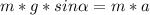, отсюда
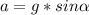--------(1)
где 
- ускорение поступательного движения цилиндра.
С другой стороны ускорение равно:
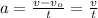-------(2)
где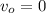 
- начальная скорость (по условию)
- скорость цилиндра через промежуток времени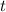 
, когда он коснется первый раз горизонтали.
Из (1) и (2) найдем искомое время :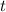
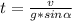---------(3)
2) Конечную скорость найдем с закона сохранения механической энергии:
![m*g*[h+R(cos\alpha-1)]=\frac{J\omega^{2}}{2}+\frac{m*v^{2}}{2}](/tpl/images/0016/7627/5d4f9.png)
------(4)
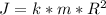------(5)
где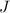 
- момент инерции цилиндра относительно его оси симметрии;
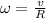--------(6)
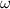- угловая скорость вращения цилиндра
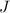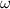Подставим в (4) вместо и выражения (5) и (6), получим после сокращения:
![g*[h+R(cos\alpha-1)]=\frac{k*v^{2}}{2}+\frac{v^{2}}{2}](/tpl/images/0016/7627/36247.png)
, отсюда
![v=\sqrt{\frac{2g*[h+R(cos\alpha-1)]}{k+1}}](/tpl/images/0016/7627/f9f05.png)
----------(7)
Подставим в (3) вместо выражение (7), получим расчетную формулу для искомого времени:
![t=\sqrt{\frac{2*[h+R(cos\alpha-1)]}{g*(k+1)sin^{2}\alpha}}](/tpl/images/0016/7627/811ed.png)
Расчет времени:
а) Для сплошного цилиндра, для которого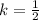 
:
![t=\sqrt{\frac{2*[0,5+6*10^{-2}(\frac{\sqrt{3}}{2}-1)]}{9,8*(\frac{3}{2})*\frac{1}{4}}\approx0,52](/tpl/images/0016/7627/53fc7.png)
с
б) Для тонкостенного цилиндра, для которого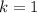 
:
![t=\sqrt{\frac{2*[0,5+6*10^{-2}(\frac{\sqrt{3}}{2}-1)]}{9,8*2*\frac{1}{4}}\approx0,45](/tpl/images/0016/7627/4afd2.png)
Дано:
S = h = 21 м
t = 420 сек
m = 500 т = 500000 кг
g = 10 H/кг
Решение
N = A/t; A = F * S;
F = m * g; N = m * g * S / t = 500000 * 10 * 21 / 420 = 250000 Вт
ответ: 250000 Вт