2. Используя объём канистры, предполагая, что бензин занимает его полностью, и найдя плотность бензина в таблице плотностей: кг/м³, можем найти массу бензина:
3. Общая масса бензина с канистрой:
4. Вес, в данной задаче равный силе тяжести, находим по формуле: где м/с² - ускорение свободного падения.
5. Объединяем всё вышенаписанное в одну формулу:
Численно получим:
(Н).
ответ: 291 Н.→ Задача #2Дано:
Жёсткость пружины: Н/м.
Удлинение пружины: см = м.
Найти нужно массу груза:
Решение:
0. Сделаем небольшой рисунок, чтобы увидеть, как и какие силы действуют на груз.
1. Распишем второй закон Ньютона для данного рисунка: где м/с² - ускорение свободного падения.
2. В проекции на ось Оу (1) перепишется так:
3. Вспоминаем классическую формулу для силы упругости:
Тут без чертежа никак: рисуем наклонную плоскость, на ней тело и расставляем силы: сила тяги вдоль наклонной плоскости вверх, сила трения вдоль плоскости, но вниз, сила тяжести приложена к центру масс тела и направлена ВЕРТИКАЛЬНО вниз, сила реакции опоры приложена к центру масс тела но ВДОЛЬ ПЕРПЕНДИКУЛЯРА К НАКЛОННОЙ ПЛОСКОСТИ. ось ОХ направляем вдоль наклонной плоскости вверх, ось ОУ вдоль вектора силы реакции опоры вверх, угол α=30 угол у основания наклонной плоскости. Теперь нам надо записать 2 закон Ньютона в векторном виде: → → → → → → Fтяг+Fтр+mg+N=ma, теперь нам надо найти проекции этих сил на координатные оси ОХ: Fтяг-Fтр - mg sinα=ma (сила трения имеет отрицательную проекцию, тк. она направлена "против" оси ОХ, mg отрицательна т.к. идем от начала проекции к концу против направления оси, а если опустить перпендикуляр из конца вектора на ОХ то получим, что угол 30 будет лежать напротив проекции, т.е сам вектор при этом будет равен mg sinα) Теперь аналогично находим проекции всех векторов на ОУ: 0+0-mg cosα+N=0 отсюда находим, что N=mg cosα, вспоминаем, что Fтр=μN=μ mg cosα, осталось все собрать в кучу, получаем: Fтяг- μ mg cosα - mg sinα=ma отсюда a=(Fтяг -μ mg cosα -mg sinα)/m=(7000-0,1*1000*10*√3/2 - 1000*10*1/2)/1000=(6150-5000)/1000=1150/1000=1,15 м/с.кв.
Длина: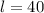 см =
см = 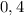 м.
м.
Высота: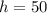 см =
см = 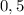 м.
м.
Ширина: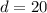 см =
см = 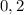 м.
м.
Масса канистры: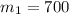 г =
г = 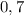 кг.
кг.
Найти нужно общий вес бензина и канистры:
Решение:1. Найдём объём канистры: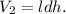
2. Используя объём канистры, предполагая, что бензин занимает его полностью, и найдя плотность бензина в таблице плотностей: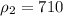 кг/м³, можем найти массу бензина:
кг/м³, можем найти массу бензина: 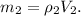
3. Общая масса бензина с канистрой: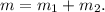
4. Вес, в данной задаче равный силе тяжести, находим по формуле: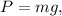 где
где 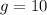 м/с² - ускорение свободного падения.
м/с² - ускорение свободного падения.
5. Объединяем всё вышенаписанное в одну формулу: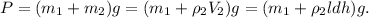
Численно получим:
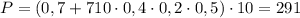 (Н).
(Н).
ответ: 291 Н.→ Задача #2Дано:Жёсткость пружины: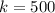 Н/м.
Н/м.
Удлинение пружины: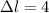 см =
см = 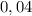 м.
м.
Найти нужно массу груза:
Решение:0. Сделаем небольшой рисунок, чтобы увидеть, как и какие силы действуют на груз.
1. Распишем второй закон Ньютона для данного рисунка: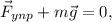 где
где 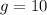 м/с² - ускорение свободного падения.
м/с² - ускорение свободного падения.
2. В проекции на ось Оу (1) перепишется так: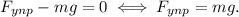
3. Вспоминаем классическую формулу для силы упругости: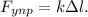
4. Объединяем (2) и (3):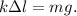
5. Выразим массу из (4):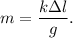
Численно получим:
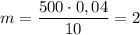 (кг).
(кг).
ответ: 2 кг.