1 Давление на опору:
По формуле давления твёрдых тел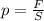 
, где F - сила давления (Н), S - площадь опоры (м²).
2 Давление столба жидкости:
По формуле давления жидкостей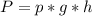 
, где р - плотность вещества (кг/м³), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). h - высота столба жидкости (м).
3 Плотность вещества:
По формуле плотности вещества 
, где m - масса тела (вещества) (кг), V - величина объёма (м³).
4 Вес тела:
По формуле веса тела 
, где m - масса тела (кг), а - ускорение тела (м/с²), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²).
5 Объем цилиндра:
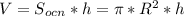, где h - высота цилиндра (м), S - площадь основания (м²).
6 Сила тяжести:
По формуле силы тяжести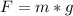 
, где m - масса тела (кг), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²).
7 Масса тела через плотность:
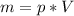, где р - плотность тела (кг/м³), V - объём тела (м³).
8 Сила давления через давление:
Такого не знаю
Записать единицы измерения величин:
1 Сила - измеряется в Ньютонах (Н)
2 Вес - измеряется в Ньютонах (Н)
3 Масса - измеряется в килограммах (кг)
4 Плотность - измеряется в килограмм на метр кубический (кг/м³)
5 Давление - измеряется в Паскалях (Па)
6 Площадь - измеряется в метрах квадратных (м²)
7 Объем - измеряется в метрах кубических (м³)
8 Скорость - измеряется в метр на секунду (м/с)
9 Путь - измеряется в метрах (м)
Перевести единицы измерения:
1 5 Н/см2 = 5*10⁴ Па
2 360 Па = 2,360 кПа
3 4,3 г/см3 = 4,3*10³ кг/м3
4 60 мм = 460*10⁻³ м
5 200 см2 = 52*10⁻² м2
6 1000 см3 = 61*10⁻³ м3
7 780 000 Па= 7,78 МПА
8 3 см = 0,83 м
9 0,6 г/см3= 90600 кг/м3
10 30 Н/см2= 1030*10⁴ Па
11 0,04 Н/см2 = 1100400 Па
12 600 см2 =1,26 м2
В 7 Па = 7*10⁻⁶ МПа.
2 ЧАСТЬ.
Записать формулы:
Смотри вверхние там тоже самое
Записать единицы измерения величин:
1 Скорость - м/с
2 Путь - м
3 Давление - Па
4 Плотность - кг/м³
5 Масса - кг
6 Площадь - м²
7 Сила - Н
8 Объем - м³
9 Вес - Н
Перевести единицы измерения:
1 0,3 Н/см2 = 3000 Па
2 86 Па = 0,286 кПа
3 6,4 г/см3 = 6400 кг/м3
4 600 мм = 4,6 м
5 25 см2 = 525*10⁻⁴ м2
6 4000 см3 = 63*10⁻³ м3
7 150 000 Па = 7,15 МПа
8 32 см = 8,32 м
9 0,06 г/см3 = 90060 кг/м3
10 300 Н/см2=10300*10⁴ Па
11 0,4 Н/см2 = 1104*10³ Па
12 400 см2 = 12,4 м2
Фаза колебаний начальная — значение фазы колебаний (полной) в начальный момент времени, т.е. при t = 0 (для колебательного процесса), а также в начальный момент времени в начале системы координат, т.е. при t = 0 в точке (x, y, z) = 0 (для волнового процесса).
Фаза колебания (в электротехнике) — аргумент синусоидальной функции (напряжения, тока), отсчитываемый от точки перехода значения через нуль к положительному значению
Как правило, о фазе говорят применительно к гармоническим колебаниям или монохроматическим волнам. При описании величины, испытывающей гармонические колебания, используется, например, одно из выражений
Аналогично, при описании волны, распространяющейся в одномерном пространстве, например, используются выражения вида
для волны в пространстве любой размерности (например, в трехмерном пространстве)
Фаза колебаний (полная) в этих выражениях — аргумент функции, т.е. выражение, записанное в скобках; фаза колебаний начальная — величина φ0, являющаяся одним из слагаемых полной фазы. Говоря о полной фазе, слово полнаячасто опускают.
Поскольку функции sin(…) и cos(…) совпадают друг с другом при сдвигеаргумента (то есть фазы) на то во избежание путаницы лучше пользоваться для определения фазы только одной из этих двух функций, а не той и другой одновременно. По обычному соглашению фазой считают аргумент косинуса.
То есть, для колебательного процесса (см. выше) фаза (полная)
для волны в одномерном пространстве
для волны в трехмерном пространстве или пространстве любой другой размерности:
,
где — угловая частота (величина, показывающая, на сколько радиан или градусов изменится фаза за 1 с; чем величина выше, тем быстрее растет фаза с течением времени); t— время; — начальная фаза (то есть фаза при t = 0); k— волновое число; x — координата точки наблюдения волнового процесса в одномерном пространстве; k — волновой вектор; r — радиус-вектор точки в пространстве (набор координат, например,декартовых).
В приведенных выше выражениях фаза имеет размерность угловых единиц (радианы, градусы). Фазу колебательного процесса по аналогии с механическим вращательным также выражают в циклах, то есть долях периода повторяющегося процесса:
1 цикл = 2 радиан = 360 градусов.
В аналитических выражениях (в формулах) преимущественно (и по умолчанию) используется представление фазы в радианах, представление в градусах также встречается достаточно часто (по-видимому, как предельно явное и не приводящее к путанице, поскольку знак градуса не принято никогда опускать ни в устной речи, ни в записях). Указание фазы в циклах или периодах (за исключением словесных формулировок) в технике сравнительно редко.
Иногда (в квазиклассическом приближении, где используются квазимонохроматические волны, т.е. близкие к монохроматическим, но не строго монохроматические) а также в формализме интеграла по траекториям, где волны могут быть и далекими от монохроматических, хотя всё же подобны монохроматическим) рассматривается фаза, являющаяся нелинейной функцией времени t и пространственных координатr, в принципе — произвольная функция