Длина волны «красной границы» фотоэффекта для некоторого вещества составляет λкр - 580 нм.
Вещество облучают излучением ,частота которого составляет ν Гц - 8.4 * 10^14.
А)Найдите работу выхода электронов из вещества ( ответ дайте в Дж и в эВ).
Б)Найдите максимальную кинетическую энергию фотоэлектронов (ответ дайте в Дж и в эВ).
В) Найдите модуль запирающего напряжения.
Г)Вычислите максимальную скорость фотоэлектронов.
Д) ответьте на во Как изменится максимальная скорость выбитых светом электронов, если фотокатод заменить другим, для которого длина волны «красной границы» фотоэффекта будет равна 0,75 λкр ? ответ пояснить, опираясь на расчеты и рассуждения.
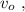

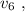
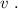
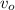 до
до  и от состояния
и от состояния  до
до  – одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное:
– одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное: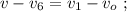 [1]
[1] до
до  – поезд проезжает расстояние вшестеро большее, чем от состояния
– поезд проезжает расстояние вшестеро большее, чем от состояния 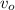 до
до 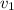 – а значит, средняя скорость
– а значит, средняя скорость  вшестеро больше средней скорости
вшестеро больше средней скорости 
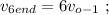
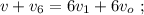
 [2]
[2]
 вагонов + локомотив.
вагонов + локомотив.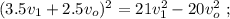
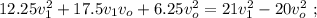
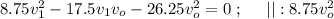
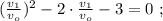
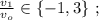
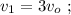
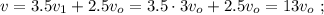

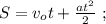
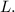
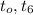 и
и 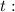
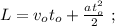 [1]
[1] [2]
[2]
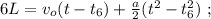
 то, используя [1]:
то, используя [1]:

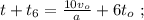
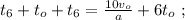
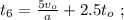
 [3]
[3]


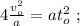
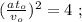
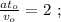

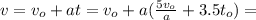
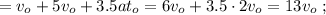

Сдѣлаемъ дополнительныя построенія въ пространствѣ и во времени. Пусть длина вагона равна
Время
Аналогично имѣемъ время
Время
Время
Изъ равенства времёнъ, имѣющагося въ условіи:
Изъ выраженій [1] и [2] съ числовымъ значеніемъ
ОТВѢТЪ :