Дано:
I₁ = 5 А
P₁ = 9,5 Вт
I₂ = 8 А
P₂ = 14,4 Вт
-----------------------
Iкз - ?
Формулы:
1) Закон Ома для участка цепи (без источника питания):

где:
I -ток в данном участке цепи, А
U -напряжение на концах этого участка, В
R -сопротивление участка цепи, Ом
2) Закон Ома для полной цепи (с источником питания):
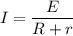
где:
I -ток в цепи, А
E -ЭДС источника питания (электродвижущая сила), В
R -внешнее сопротивление (вне источника питания), Ом
r -внутреннее сопротивление источника питания, Ом
Ток короткого замыкания вычисляется по этой же формуле, но внешнее сопротивление исключается (делается равным нулю).
3) Расчёт мощности:
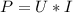
где:
P -мощность, рассеиваемая в цепи, Вт
U -напряжение, приложенное к данной цепи, В
I -ток в цепи, А
Используя формулу (3) выразим и найдём напряжение, приложенное к внешней цепи (напряжение на выходе источника питания):
 В
В
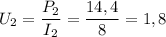 В
В
Используя формулу (1) выразим и найдём сопротивление внешней цепи:
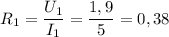 Ом
Ом
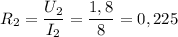 Ом
Ом
Из формулы (2) выразим ЭДС и запишем это выражение для первого и второго измерения:
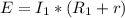

Так как ЭДС и внутреннее сопротивление не меняются от тока (это всегда одни и те же характеристики батареи), то мы можем составить уравнение, приравняв правые части этих двух выражений:

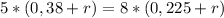
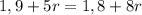
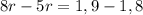
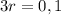
 Ом
Ом
Вычислим ЭДС по одному из ранее записанных выражений:
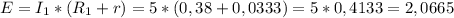 В
В
Вычислим ток короткого замыкания:
Iкз = E / r = 2,0665 / 0,0333 ≈ 62,06 А
ответ: ток короткого замыкания аккумуляторной батареи равен 62,06 А
связи ядра изотопа углерода C616, если дефект массы ядра иона
Δm= 0,11558 а. е. м.
(ответ запиши с точностью до сотых).
ответ: f = (пропуск) МэВ.
2) Выбери правильный ответ.
Из приведённых ниже частиц изотопами являются
H1\1,H1\2,H1\3
e1\0,e−1\0
n0\1,p1\1,e−1\0
Be5\10,B5\10,B5\10r
3)Запиши, чему равно зарядовое и массовое число изотопа O822.
Z — число, Z=(пропуск);
A — число, A=(пропуск).
4)Вычисли массу ядра изотопа Cu. Известно, что нейтронов в ядре изотопа на k = 3меньше, чем протонов. Определи зарядовое и массовое число изотопа.
Массу одного нуклона можно принять равной m1 = 1,67⋅10−27 кг
(Массу вычисли с точностью до сотых).
ответ: ядро изотопа Cu (пропуск )имеет массу m = (пропуск) кг.
5)Вычислите энергию связи нуклонов в ядре атома изотопа углерода C68.
Масса ядра изотопа углерода равна m = 8,037675 а. е. м.
Масса свободного протона равна mp = 1,00728 а. е. м.
Масса свободного нейтрона равна mn = 1,00866 а. е. м.
(ответ запиши с точностью до десятых).
ответ: ΔE = (пропуск) МэВ.
6)Чему равна масса ядра изотопа углерода C616, если удельная энергия связи ядра изотопа ΔE = 107,7 MэВ.
Масса свободного протона равна mp = 1,00728 а. е. м.
Масса свободного нейтрона равна mn = 1,00866 а. е. м.
(ответ запиши с точностью до стотысячных, т. е. пять цифр после запятой).
ответ: m = (пропуск) а. е. м.
7)Вычислите удельную энергию связи нуклонов в ядре атома изотопа азота N722.
Масса ядра изотопа азота равна m = 22,03439 а. е. м.
Масса свободного протона равна mp = 1,00728 а. е. м.
Масса свободного нейтрона равна mn = 1,00866 а. е. м.
(ответ запиши с точностью до десятых).
ответ: f = (пропуск) МэВ.
8)Вычисли, какая энергия потребовалась бы для разделения m = 1 г ядер фтора F924 на составляющие ядро протоны и нейтроны. Рассчитай, сколько килограммов каменного угля потребуется сжечь для получения такой энергии.
Удельная теплота сгорания каменного угля равна q = (33 000 кДж/кг.
Масса ядра изотопа фтора равна mя = 24,00812 а. е. м.
Масса свободного протона равна mp = 1,00728 а. е. м.
Масса свободного нейтрона равна mn = 1,00866 а. е. м.
(Значение энергии округли до сотых, массу угля округли до десятых).
ответ: энергия, необходимая для расщепления фтора, т. е. E = (пропуск) ⋅1011 Дж
2100
Объяснение:
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
2 (1).svg
Точка нахождения тела
Потенциальная энергия
Кинетическая энергия
Полная механическая энергия
3) Самая верхняя
(h = max)
Eпот = m⋅g⋅h (max)
Eкин = 0
Eполная = m⋅g⋅h
2) Средняя
(h = средняя)
Eпот = m⋅g⋅h
Eкин = m⋅v22
Eполная = m⋅v22 + m⋅g⋅h
1) Самая нижняя
(h = 0)
Eпот = 0
Eкин = m⋅v22 (max)
Eполная = m⋅v22
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
vmax=2⋅g⋅hmax−−−−−−−−−√ .
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
hmax=v2max2g .
Видео: «Демонстрация изменения кинетической и потенциальной энергии тела при подвеса»
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
3 (1).svg
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна нулю . Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна нулю . Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся неизменной во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
4.svg
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.