Объем шара, видимо, 1000 м³...))
На воздушный шар действуют две силы: сила Архимеда, направленная вверх
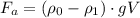
где ρ₀ = 1,29 кг/м³ - плотность воздуха
ρ₁ = 0,18 кг/м³ - плотность гелия
и сила тяжести, направленная вниз
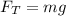
где m = 200 кг - масса оболочки шара.
Подъемная сила шара, как результирующая этих двух сил:
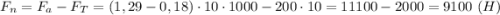
Грузоподъемность шара, таким образом:
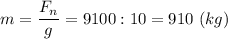
--------------------------------------
По поводу второй проблемы.
Решение то же. Вес оболочки шарика, к сожалению, все же придется вычесть из силы Архимеда, действующей на шарик. Тогда и получите подъемную силу. То, что написали Вы, - формула только для силы Архимеда, без учета веса оболочки шарика.
Был открыт Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Важно отметить, что для того, чтобы закон был верен, необходимы:
1.точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
2.их неподвижность. Иначе уже надо учитывать дополнительные эффекты: возникающее магнитное поле движущегося заряда и соответствующую ему дополнительную силу Лоренца, действующую на другой движущийся заряд.
3.взаимодействие в вакууме.
Однако, с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
где F1,2— сила, с которой заряд 1 действует на заряд 2; q1,q2 — величина зарядов; — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — r12); k — коэффициент пропорциональности. Таким образом, закон указывает, что одноименные заряды отталкиваются (а разноименные – притягиваются) .