Масса: m = 25 г = 0,025 кг.
Начальная температура льда: t₁ = -5 °C.
Температура плавления льда: t₂ = 0 °C.
Температура кипения воды: t₃ = 100 °C.
Конечная температура пара: t₄ = 110 °C.
Удельная теплоёмкость воды: c = 4200 Дж/(кг × °С).
Найти нужно общую теплоту: Q - ?
Решение:1. Общая теплота состоит из теплоты нагревания льда до температуры плавления, теплоту плавления льда, теплоты нагревания воды до температуры кипения, теплоты парообразования воды и теплоты нагревания пара до конечной температуры, получаем следующую формулу: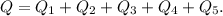 
2. Теплота нагревания льда: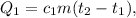 
где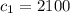 
Дж/(кг × °С) - удельная теплоёмкость льда.
3. Теплота плавления льда: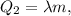 
где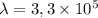 
Дж/кг - удельная теплота плавления льда.
4. Теплота нагревания воды: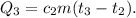 
где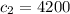 
Дж/(кг × °С) - удельная теплоёмкость льда.
5. Теплота парообразования воды: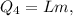 
где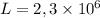 
Дж/кг - удельная теплота парообразования воды.
6. Теплота нагревания пара: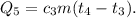 
где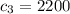 
Дж/(кг × °С) - удельная теплоёмкость пара.
7. Итоговая формула: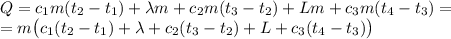 
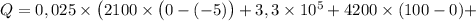
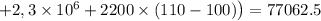(Дж).
Переведём в килоджоули: Q = 77062.5 Дж ≈ 77,1 кДж.
ответ: 77,1 кДж.
Дано:
m₁ = 1 кг
v₁ = 4 м/с
m₂ = 3 кг
v₂ = 0
соударение абсолютно упругое
Найти:
u₁ и u₂ - скорости шариков после соударения
импульс системы шариков до соударения равен
р₁ = m₁v₁
Импульс системы шариков после соударения
р₂ = m₁u₁ + m₂u₂
Закон сохранения импульса
р₁ = р₂
m₁v₁ = m₁u₁ + m₂u₂
4 = u₁ + 3u₂
или
u₁ = 4 - 3u₂ (1)
Закон сохранения энергии
0,5 m₁v₁² = 0.5m₁u₁² + 0.5m₂u₂²
или
m₁v₁² = m₁u₁² + m₂u₂²
16 = u₁² + 3u₂² (2)
Подставим (1) в уравнение (2)
16 = (4 - 3u₂)² + 3u₂²
16 = 16 - 24u₂ + 9u₂² + 3u₂²
-24u₂ + 12u₂² = 0
u₂ ≠ 0, поэтому
-2 + u₂ = 0
u₂ = 2 (м/с)
Их (1) получим
u₁ = 4 - 3 · 2 = - 2 (м/с)
1-й шарик отскочит назад со скоростью 2 м/с, а 2-й шарик покатится в направлении движения первого шарика до удара со скоростью 2 м/с.