Рассмотрим эти два движения по отдельности:
1. Законы движения тела по осям x, y:
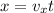
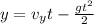
Так как угол = 45, то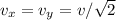 
Падение будет там, где y=0, обозначим время падения как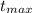 
, тогда оно будет равно:
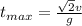
Подставим это в формулу для координаты x, найдем дистанцию броска.
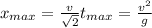
2. Закон движения по оси x (по другой оси движения нет):
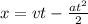
Ускорение найдем из второго закона Ньютона:
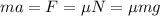, так как действующая на тело сила по оси x это сила трения, равная μN.
Чтобы найти точку остановки вспомним, что движение является равнозамедленным и в конечной точке скорость = 0. Скорость же выражается так:
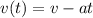
Тогда время на бросок:
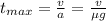
Подставляя в формулу для координаты x, получим:
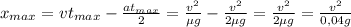
Итого, сравнивая расстояние 1 и расстояние 2, заключаем, что во втором случае тело пролетит гораздо дальше.
Сила тяги: Fт = 650 кН = 6,5 × 10⁵ Н.
Масса: m = 3250 т = 3,25 × 10⁶ Н.
Коэффициент сопротивления: μ = 0,005.
Нужно записать уравнение зависимости скорости от времени.
Решение:1. Уравнение зависимости скорости от времени в общем виде: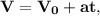
значит, чтобы его записать, нам необходимо знать ускорение и начальную скорость. Про начальную скорость ничего не сказано, принимаем 
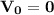м/с.
2. Сделаем рисунок, чтобы лучше понимать задачу (см. приложение). Далее будем расписывать второй закон Ньютона по осям.
3. Запишем силы, действующие на тело по оси Oy: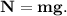
4. Запишем силы, действующие на тело по оси Ox: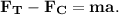
5. Сила сопротивления по определению и с учётом (3):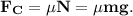
6. Объединяем (4) и (5):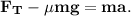
7. Выразим ускорение из (6):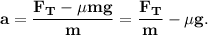
Численно получим:Итак, имеем: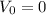
м/с, 
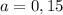м/с².
ответ: