ответ: 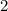 °С
°С
Объяснение:
Дано:
 °С
°С
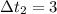 °С
°С
------------------
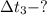
Пусть 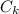 - теплоемкость калориметра
- теплоемкость калориметра
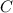 - теплоемкость воды в ложке
- теплоемкость воды в ложке
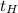 - начальная температура калориметра
- начальная температура калориметра
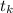 - конечная температура калориметра
- конечная температура калориметра
 - температура воды в ложке
- температура воды в ложке
Теперь запишем уравнение теплового баланса после того как мы влили первую ложку воды в пустой калориметр
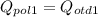
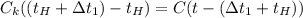
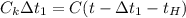 - уравнение (1)
- уравнение (1)
Аналогично и для второго случая
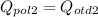
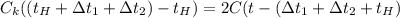
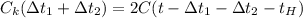 - уравнение (2)
- уравнение (2)
В уравнении (2) фигурирует 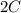 так как это уже "вторая ложка"
так как это уже "вторая ложка"
Получаем систему из уравнений (1) и (2)
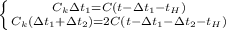
Разделим уравнение уравнение (1) на (2)
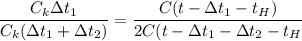
Подставляя численные значения упростим
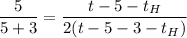
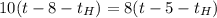
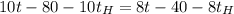
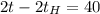
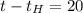 °С
°С
Тогда подставляя это в уравнение в уравнение (1) получим
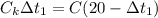
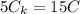
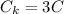
После вливания в калориметр третьей ложки получим что
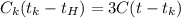
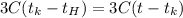
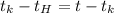
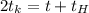
Если 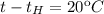 то
то 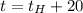
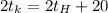
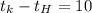 °С
°С
Допустим 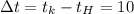 °С
°С
Тогда
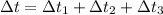
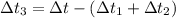
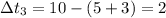 °С
°С
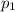 = 37 кПа
= 37 кПа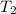 =
= 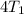
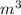
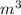
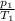 = \frac{p _{2} }{ T_{2} }
= \frac{p _{2} }{ T_{2} } 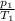 = \frac{p _{2} }{ T_{2} } ⇒ 4*
= \frac{p _{2} }{ T_{2} } ⇒ 4* *
*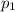 =
=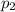 *
*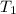 ⇒
⇒ 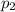 =148000Па
=148000Па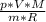 ⇒ T=398К=
⇒ T=398К=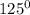 С
С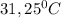
 ), где с-удельная теплоемкость гелия при постоянном давлении =
), где с-удельная теплоемкость гелия при постоянном давлении = 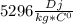
Расстояние от зеркала до изображения равно расстоянию от зеркала до объекта
r=2l= 2m
r = 2l=2*0.6 =1.2
Объяснение: