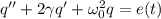, полученным из уравнения Кирхгофа введением обозначений: 
, 
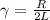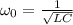. Для выяснения резонансной частоты возьмем вынуждающую силу, изменяющуюся по закону косинуса. 
.
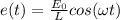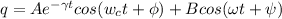, где первое слагаемое - решение с.о.у. (оно затухает и нас не интересует), а второе - произвольное частное решение, которое ищется в указанном виде (в силу особенностей взятой вынуждающей силы). Подставим решение 
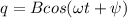в уравнение и (с например, векторной диаграммы) получим 
.
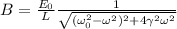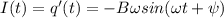и 
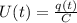. Получаем для амплитуды тока и напряжений следующие выражения: 
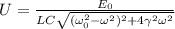и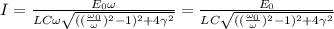 
.
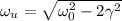, а у тока при 
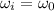.![q = Ae^{-\gamma t}cos(w_c t + \phi)[\tex] Условились считать, что колебание затухло, если его амплитуда уменьшилась в e раз. Очевидно, что это произойдёт за время [tex]\tau = \frac{1}{\gamma}](/tpl/images/0411/3944/118a7.png)
. За это время система совершила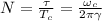 
колебаний, где 
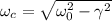- собственная частота колебаний системы (следует из решения д.у.). Так вот, величина 
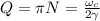называется добротностью контура.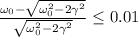
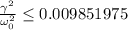, отсюда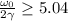 
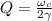и ![\frac{\omega_0}{2\gamma}[\tex] разные величины, поэтому оценим погрешность, что бы приравнять их с чистой совестью)))) Для этого разложим выражение для добротности, с учётом определения частоты собственных колебаний по формуле Маклорена (в ряд). [tex]Q = \frac{ \sqrt{\omega_0^2 - \gamma^2}}{2\gamma} = \frac{\omega_0}{2\gamma} \sqrt{1 - \frac{\gamma^2}{\omega_0^2}} = \frac{\omega_0}{2\gamma} ( 1 - \frac{\gamma^2}{2\omega_0^2} + o(\frac{\gamma^2}{\omega_0^2})) = \frac{\omega_0}{2\gamma} - \frac{\gamma}{4\omega_0} + o(\frac{\gamma}{\omega_0}).](/tpl/images/0411/3944/feb4a.png)
Таким образом, отличие истинного решения от полученного примерно 0.03.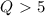
2. Давление равно сила делённая на площадь. В данном случае сила равна силе тяжести. Для расчёта сила тяжести нам необходимо знать массу, так как мы не можем высчитать массу воды мы распишем массу как произведение плотности на объем. Далее так как мы не знаем объема, распишем объем через произведение площади основания на высоту. Площади сокращаются и остается, что бавление равно произведению плотности на глубину и на девять целых восемь десятых